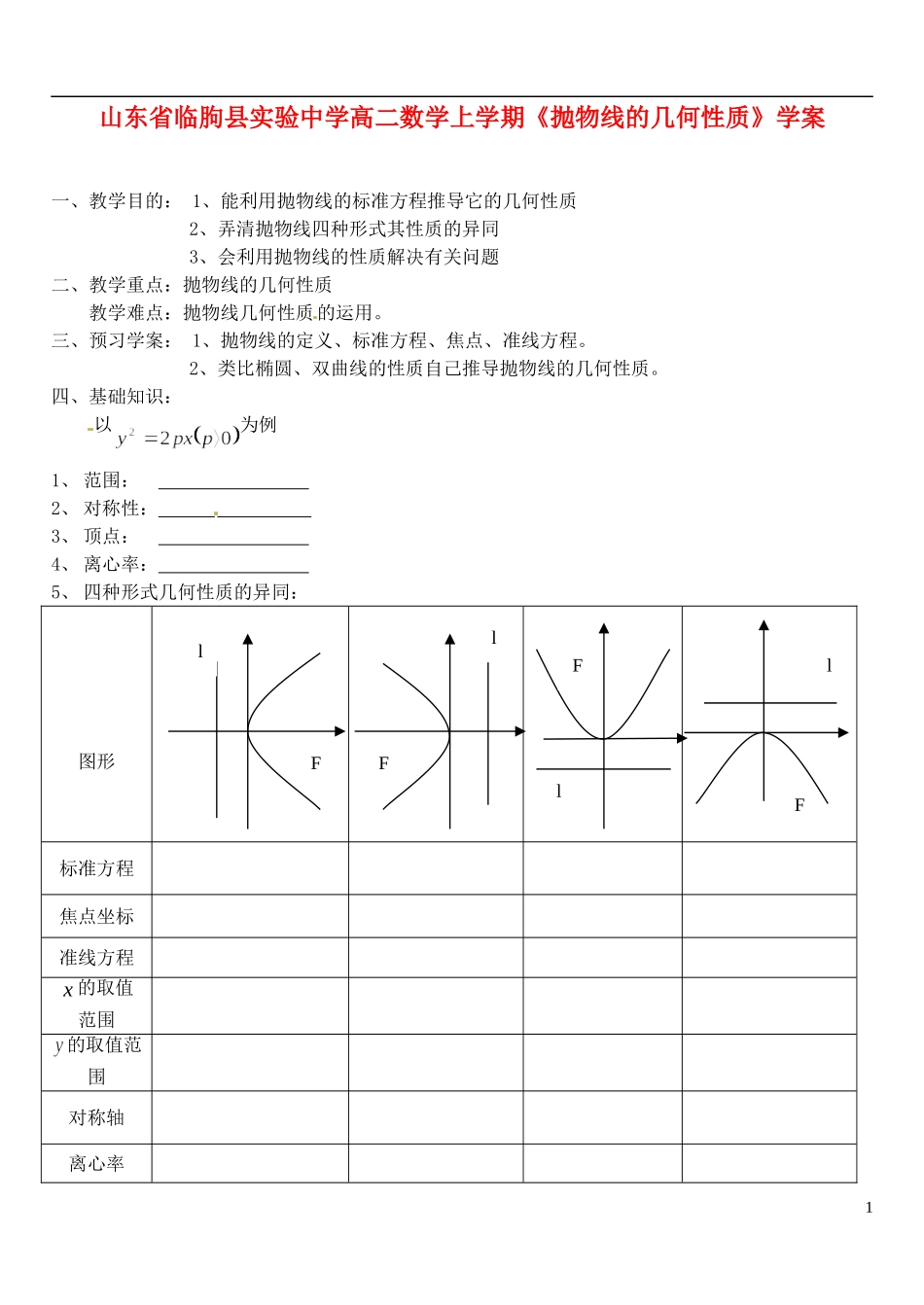
山东省临朐县实验中学高二数学上学期《抛物线的几何性质》学案一、教学目的: 1、能利用抛物线的标准方程推导它的几何性质2、弄清抛物线四种形式其性质的异同3、会利用抛物线的性质解决有关问题二、教学重点:抛物线的几何性质教学难点:抛物线几何性质的运用。三、预习学案: 1、抛物线的定义、标准方程、焦点、准线方程。2、类比椭圆、双曲线的性质自己推导抛物线的几何性质。四、基础知识:以为例1、 范围: 2、 对称性: 3、 顶点: 4、 离心率: 5、 四种形式几何性质的异同:图形标准方程焦点坐标准线方程x 的取值范围的取值范围对称轴离心率1FlFlFFll的焦半径6、 焦半径:抛物线上一点 M 与焦点 F 连线的线段叫做焦半径。设抛物线上一点 M(x,y)由抛物线的定义,易知7、 焦点弦:过焦点的弦设 AB是过抛物线焦点 F 的一条弦,则有:① ②特别地,当焦点弦垂直于对称轴时,又称作正焦弦(“通径”)此时,从而 p 刻画了抛物线开口大小,p 越大,开口越宽.p 越小,开口越窄.五、典型例题 (一)利用性质求抛物线标准方程例 1、抛物线以 轴为轴,顶点在坐标原点,开口向右,且过,求抛物线的标准方程.若抛物线顶点在坐标原点,过,该抛物线标准方程为练习:抛物线以 轴为轴,顶点在坐标原点,且顶点与焦点的距离等于 3,则抛物线标准方程为2(二)焦点弦问题例 2、已知抛物线过焦点的弦为,且,求中点的横坐标.练 习 : 已 知是 抛 物 线上 三 点 ,为 焦 点 , 若成等差数列。证明:(三)抛物线中的最值问题例 3、已知抛物线。(1)设点,求抛物线上距离点最近的点的坐标及相应的距离(2)在抛物线上求一点,使到直线的距离最短,并求出距离的最小值。3练习:课本当堂检测:1、抛物线的准线方程为,则 2、边长为 1 的等边三角形,为原点,轴,以为顶点且过的抛物线方程是 3、抛物线的顶点在原点,焦点在 轴上,其上有一点,其到准线的距离为 6,则 4、过的直线与抛物线交于两点,若线段中点的横坐标为 2,则 5、 抛物线上的点到直线的距离的最小值为 6、 已知点,是抛物线上任意一点,为焦点,则的最小值为 此时的坐标为 7、 设点,点在轴上,且,当点在轴上运动时,求点的轨迹方程。8、 过抛物线的焦点的直线交抛物线于两点,证明: 4