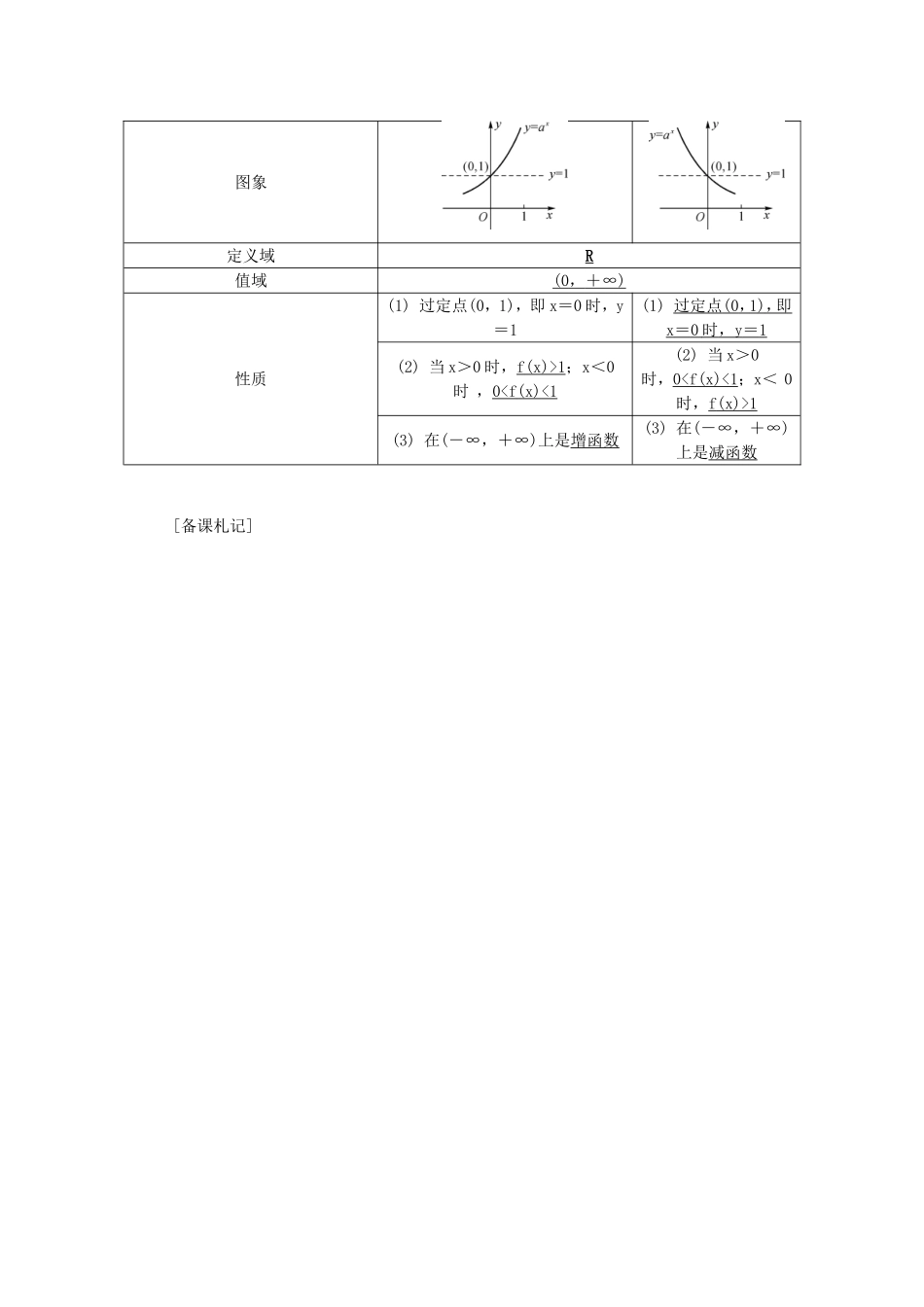
第二章函数与导数第8课时指数函数、对数函数及幂函数(2)第三章(对应学生用书(文)、(理)22~23页)考情分析考点新知高考对指数函数的考查近三年有所升温,重点是指数函数的图象和性质,以及指数函数的实际应用问题,在复习时要特别重视对指数函数性质的理解与应用.①了解指数函数模型的实际背景.②理解指数函数的概念,并理解指数函数的单调性与函数图象通过的特殊点.③知道指数函数是一类重要的函数模型.1.(必修1P110复习9改编)函数y=ax-3+3恒过定点________.答案:(3,4)解析:当x=3时,f(3)=a3-3+3=4,∴f(x)必过定点(3,4).2.(必修1P110复习3改编)函数y=的定义域是________.答案:解析:由8-16x≥0,所以24x≤23,即4x≤3,定义域是.3.(必修1P67练习3)函数f(x)=(a2-1)x是R上的减函数,则a的取值范围是________________.答案:(-,-1)∪(1,)解析:由0<a2-1<1,得1<a2<2,所以1<|a|<,即-<a<-1或1<a<.4.(必修1P71习题13改编)已知函数f(x)=a+是奇函数,则常数a=________.答案:-解析:由f(-x)+f(x)=0,得a=-.5.(原创)函数y=1+|x-1|的值域为__________.答案:(1,2]解析:设y′=u,u=|x-1|.由于u≥0且y′=u是减函数,故0<|x-1|≤1,则1<y≤2.1.指数函数定义一般地,函数y=ax(a>0,a≠1)叫做指数函数,函数的定义域是R.2.指数函数的图象与性质a>10
1;x<0时,01(3)在(-∞,+∞)上是增函数(3)在(-∞,+∞)上是减函数[备课札记]题型1指数型函数的定义域、值域例1已知x∈[-3,2],求f(x)=-+1的最小值与最大值.解:f(x)=-+1=4-x-2-x+1=2-2x-2-x+1=2+. x∈[-3,2],∴≤2-x≤8.则当2-x=,即x=1时,f(x)有最小值;当2-x=8,即x=-3时,f(x)有最大值57.已知9x-10×3x+9≤0,求函数y=-4+2的最大值和最小值.解:由9x-10·3x+9≤0,得(3x-1)(3x-9)≤0,解得1≤3x≤9,∴0≤x≤2.令()x=t,则≤t≤1,y=4t2-4t+2=4(t-)2+1,当t=即x=1时,ymin=1;当t=1即x=0时,ymax=2.题型2指数型函数的图象例2已知函数f(x)=|2x-1-1|.(1)作出函数y=f(x)的图象;(2)若af(c),求证:2a+2c<4.(1)解:f(x)=其图象如图所示.(2)证明:由图知,f(x)在(-∞,1]上是减函数,在[1,+∞)上是增函数,故结合条件知必有a<1.若c≤1,则2a<2,2c≤2,所以2a+2c<4;若c>1,则由f(a)>f(c),得1-2a-1>2c-1-1,即2c-1+2a-1<2,所以2a+2c<4.综上知,总有2a+2c<4.画出函数y=的图象,并利用图象回答:k为何值时,方程=k无解?有一个解?有两个解?解:.由图知,当k<0时,方程无解;当k=0或k≥1时,方程有一个解;当00且a≠1).(1)求函数f(x)的定义域;(2)讨论函数f(x)的奇偶性;(3)求a的取值范围,使f(x)>0在定义域上恒成立.解:(1)由于ax-1≠0,则ax≠1,所以x≠0,所以函数f(x)的定义域为{x|x∈R,且x≠0}.(2)对于定义域内任意的x,有f(-x)=(+)(-x)3=-x3=-x3=x3=f(x),所以f(x)是偶函数.(3)①当a>1时,对x>0,所以ax>1,即ax-1>0,所以+>0.又x>0时,x3>0,所以x3>0,即当x>0时,f(x)>0.由(2)知,f(x)是偶函数,即f(-x)=f(x),则当x<0时,-x>0,有f(-x)=f(x)>0成立.综上可知,当a>1时,f(x)>0在定义域上恒成立.②当00时,00,有f(-x)=f(x)<0,也不满足题意.综上可知,所求a的取值范围是a>1.设a>0,f(x)=+是R上的偶函数.(1)求a的值;(2)判断并证明函数f(x)在[0,+∞)上的单调性;(3)求函数的值域.解:(1)因为f(x)为偶函数,故f(1)=f(-1),于是+=+3a,即=.因为a>0,故a=1.(2)设x2>x1≥0,f(x1)-f(x2)=(3x2-3x1)(-1).因为3x为增函数,且x2>x1,故3x2-3x1>0.因为x2>0,x1≥0,故x2+x1>0,于是<1,即-1<0,所以f(x1)-f(x...