第二章函数与导数第9课时指数函数、对数函数及幂函数(3)第三章(对应学生用书(文)、(理)24~25页)考情分析考点新知①对数函数在高考中的考查主要是图象和性质,同时考查数学思想方法,以考查分类讨论及运算能力为主;考查形式主要是填空题,同时也有综合性较强的解答题出现,目的是结合其他章节的知识,综合进行考查.②幂函数的考查较为基础,以常见的5种幂函数为载体,考查求值、单调性、奇偶性、最值等问题是高考命题的出发点.①理解对数函数的概念;理解对数函数的单调性;掌握对数函数图象通过的特殊点.②知道对数函数是一类重要的函数模型.③了解指数函数y=ax与对数函数y=logax的相互关系(a>0,a≠1).④了解幂函数的概念,结合函数y=x,y=x2,y=x3,y=x-1,y=x-2的图象,了解它们的变化情况.1.(必修1P112测试8改编)已知函数f(x)=logax(a>0,a≠1),若f(2)>f(3),则实数a的取值范围是________.答案:(0,1)解析:因为f(2)>f(3),所以f(x)=logax单调递减,则a∈(0,1).2.(必修1P89练习3改编)若幂函数y=f(x)的图象经过点,则f(25)=________.答案:解析:设f(x)=xα,则=9α,∴α=-,即f(x)=x-,f(25)=.3.(必修1P111习题15改编)函数f(x)=ln是________(填“奇”或“偶”)函数.答案:奇解析:因为f(-x)=ln=ln=-ln=-f(x),所以f(x)是奇函数.4.(必修1P87习题13改编)不等式lg(x-1)<1的解集为________.答案:(1,11)解析:由0
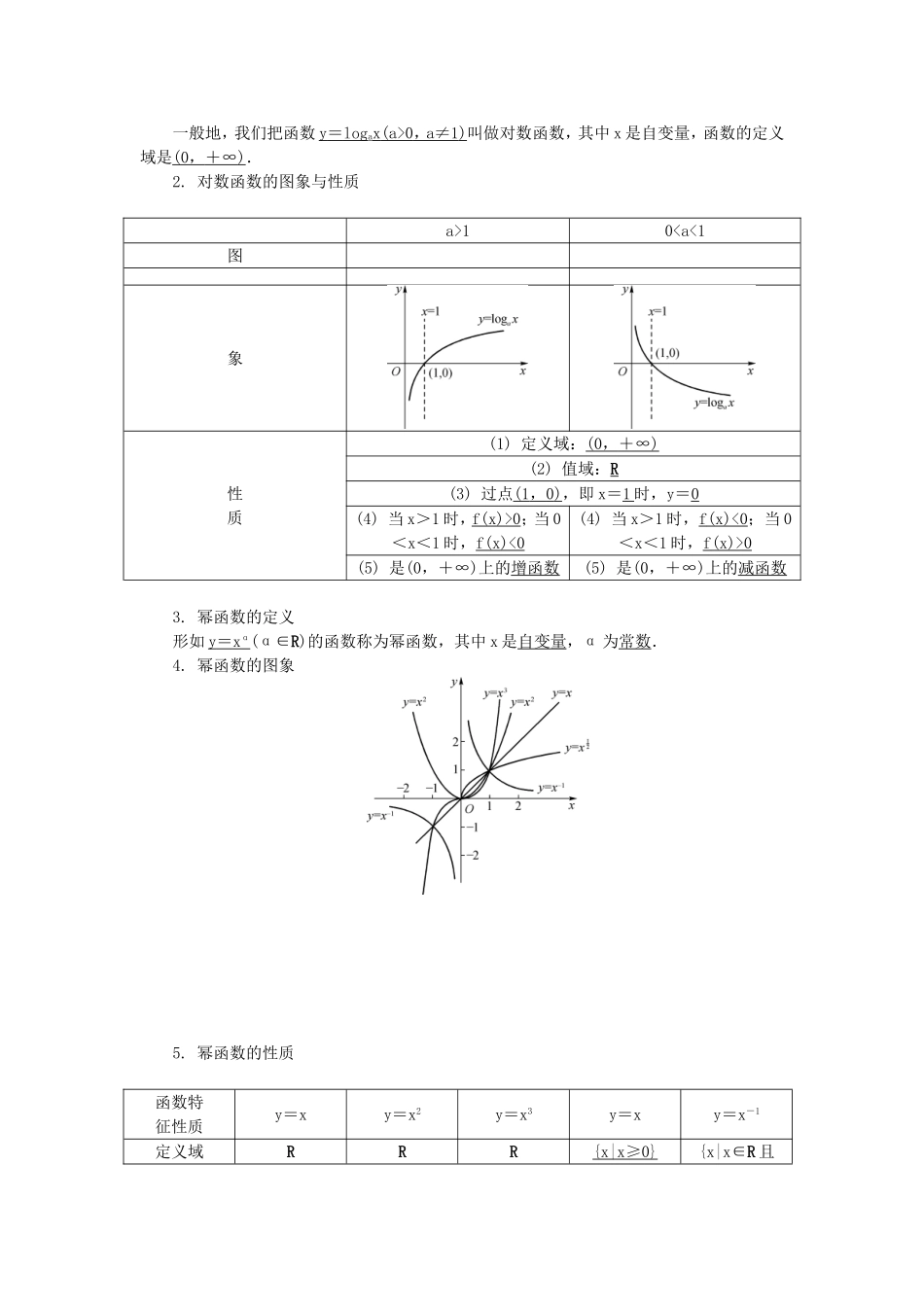
0,a≠1)叫做对数函数,其中x是自变量,函数的定义域是(0,+∞).2.对数函数的图象与性质a>100;当0<x<1时,f(x)<0(4)当x>1时,f(x)<0;当0<x<1时,f(x)>0(5)是(0,+∞)上的增函数(5)是(0,+∞)上的减函数3.幂函数的定义形如y=xα(α∈R)的函数称为幂函数,其中x是自变量,α为常数.4.幂函数的图象5.幂函数的性质函数特征性质y=xy=x2y=x3y=xy=x-1定义域RRR{x|x≥0}{x|x∈R且x≠0}值域R{y|y≥0}R{y|y≥0}{y|y∈R且y≠0}奇偶性奇偶奇非奇非偶奇单调性增(-∞,0]减,[0,+∞)增增增(-∞,0)减,(0,+∞)减定点(1,1)[备课札记]题型1对数函数的概念与性质例1(1)设a>1,函数f(x)=logax在区间[a,2a]上的最大值与最小值之差是,则a=________;(2)若a=log0.40.3,b=log54,c=log20.8,用小于号“<”将a、b、c连结起来________;(3)设f(x)=lg是奇函数,则使f(x)<0的x的取值范围是________;(4)已知函数f(x)=|log2x|,正实数m、n满足m1,∴函数f(x)=logax在区间[a,2a]上是增函数,∴loga2a-logaa=,∴a=4.(2)由于a>1,01,且mn=1,所以f(m2)=|log2m2|=2,解得m=,所以n=2.(1)设loga<1,则实数a的取值范围是________;(2)已知函数f(x)=lg(x2+t)的值域为R,则实数t的取值范围是________;(3)若函数f(x)=loga|x+1|在(-1,0)上有f(x)>0,则函数f(x)的单调减区间是________;(4)若函数f(x)=log(x2-2ax+3)在(-∞,1]内为增函数,则实数a的取值范围是________.答案:(1)0<a<或a>1(2)a≤0(3)(-1,+∞)(4)[1,2)解析:(1)分a>1与a<1两种情形进行讨论.(2)值域为R等价于x2+a可以取一切正实数.(3)函数f(x)的图象是由y=loga|x|的图象向左平移1个单位得到,∴0