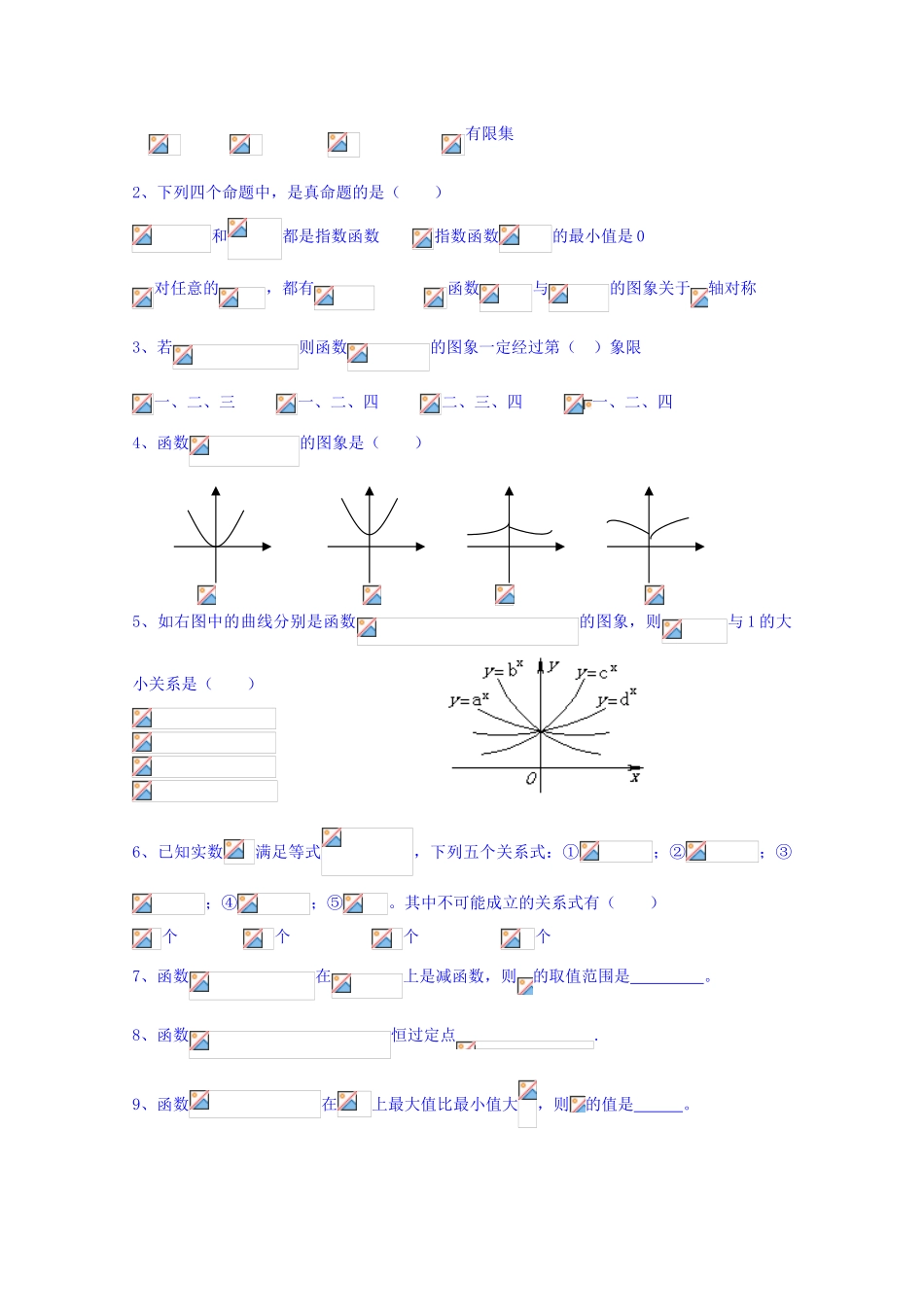
山东省聊城市第四中学 2014-2015 学年高三数学一轮复习 2.8 指数函数及其性质学案一、高考目标:1、了解指数函数模型的实际背景.2、理解指数函数的概念,理解指数函数的单调性,掌握指数函数图象通过的特殊点.3、知道指数函数是类重要的函数模型.二、知识再现:1、指数函数的定义:一般地,函数 叫做指数函数,其中 是自变量,定义域为 .2、指数函数的图像与性质如下表所示: 图象 定义域 值域性质 (1)过定点 ,即 时, .(2)当时, ,当 时,.(2)当时, ,当 时,.(3)在 上是增函数(3)在上是 三、考点例析:例 1、已知。(1)判断函数的奇偶性;(2)讨论的单调性;(3)求的值域。例 2、当时,求函数的最大值及最小值.变式训练:(1)已知函数,求使恒成立的的取值范围.四、达标训练:1、集合,则是( ) 有限集2、下列四个命题中,是真命题的是( )和都是指数函数 指数函数的最小值是 0对任意的,都有 函数与的图象关于轴对称3、若则函数的图象一定经过第( )象限一、二、三 一、二、四 二、三、四 一、二、四4、函数的图象是( ) 5、如右图中的曲线分别是函数的图象,则与 1 的大小关系是( ) 6、已知实数满足等式,下列五个关系式:①;②;③;④;⑤。其中不可能成立的关系式有( )个 个 个 个7、函数在上是减函数,则的取值范围是 。8、函数恒过定点.9、函数在上最大值比最小值大,则的值是 。10、将按从小到大的顺序排列为 。已知函数的定义域是,则函数的定义域是 。11、函数的单调递增区间是。12、若直线与函数且的图象有两个公共点,则的取值范围是 。