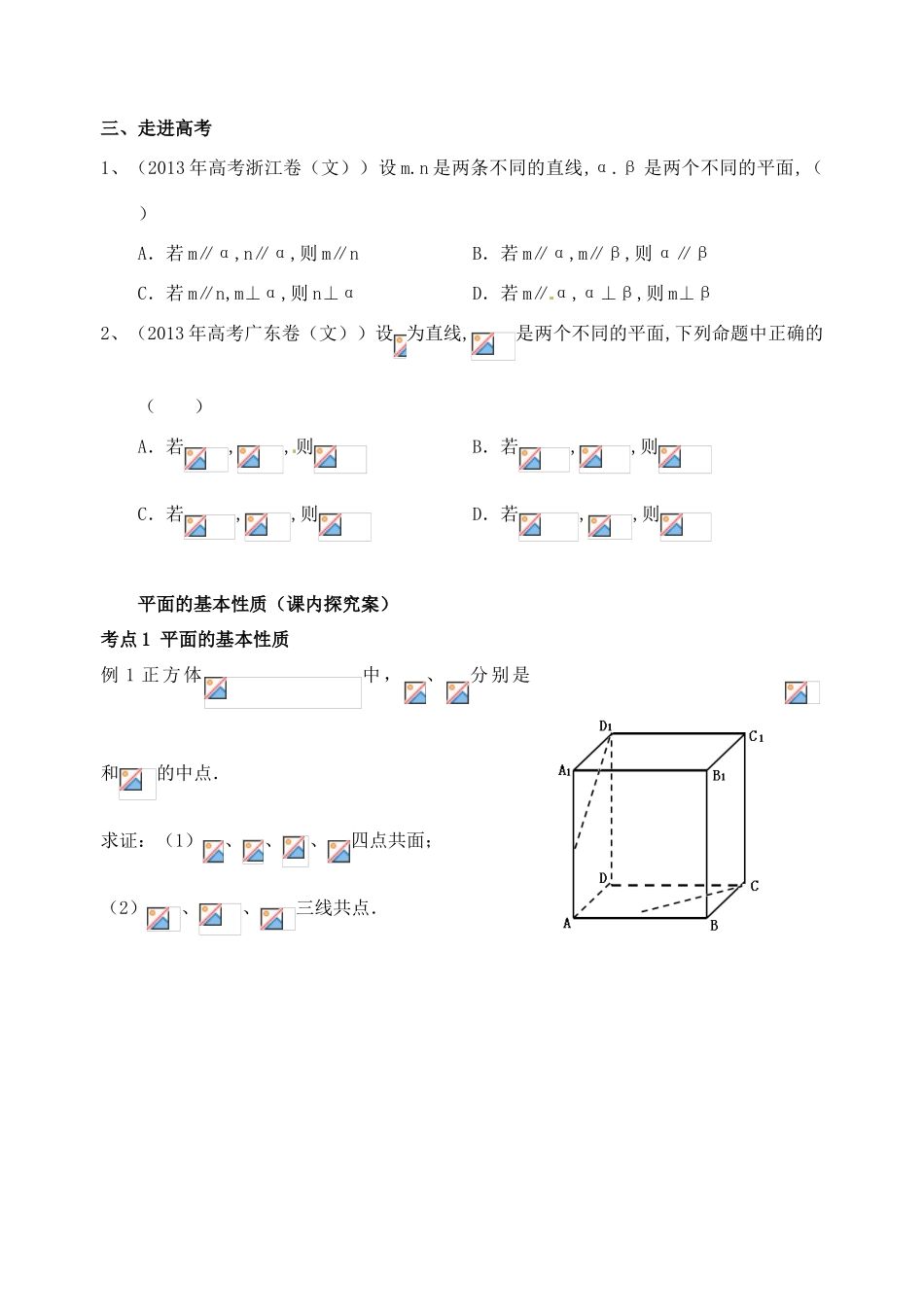
山东省高密市第三中学高三数学 7.1 平面基本性质与推论复习导学案一、高考命题分析从近几年高考题来看,对本节内容的考查主要是:(1)空间点、线、面的位置关系;(2)异面直线所成的角.二、【知识回顾】1.平面的基本性质:公理 1 :如果一条直线上的 在一个平面内,那么这条直线在这个平面内.公理 2:过 的三点,有且只有一个平面.公理 3:如果两个不重合的平面有一个公共点,那么它们有且只有 过该点的公共直线.2.直线与直线的位置关系(1)位置关系的分类:(2)异面直线所成的角① 定义:设,是两条异面直线,经过空间中任一点作直线,,把与所成的 叫做异面直线,所成的角(或夹角).② 范围: .3.直线与平面的位置关系 、 、 三种情况.4.平面与平面的位置关系 、 两种情况.5.平行公理平 行于 的两条直线互相平行.6.定理空间中如果两个角的两边分别对应平行,那么这两个角 .三、走进高考1、(2013 年高考浙江卷(文))设 m.n 是两条不同的直线,α.β 是两个不同的平面,( )A.若 m∥α,n∥α,则 m∥nB.若 m∥α,m∥β,则 α∥β C.若 m∥n,m⊥α,则 n⊥αD.若 m∥α,α⊥β,则 m⊥β2、(2013 年高考广东卷(文))设 为直线,是两个不同的平面,下列命题中正确的( )A.若,,则B.若,,则 C.若,,则D.若,,则平面的基本性质(课内探究案)考点 1 平面的基本性质例 1 正方体中,、分别是和的中点.求证:(1)、、、四点共面;(2)、、三线共点.变式 1:正方体中,、、分别是、、的中点,那么正方体的过、、的截面图形是( )A.三角形B.四边形C.五边形D.六边形考点 2 空间线面的位置关系例 2 如图所示,正方体中,、分别是、的中点.问:(1)和是否是异面直线?说明理由;(2)和是否是异面直线.变式 2 用、、表示三条不同的直线,表示平面,给出下列命题:① 若,,则;②若,,则;③若,,则;④若,,则.其中真命题的序号是( )A.①②B.②③C.①④D.③④【当堂检测】1.若直线,,则直线与的位置关系是( )A.异面B.相交C.平行D.异面或相交2.平行六面体中,既与共面,又与共面的棱的条数为 .平面的基本性质(课后巩固案)A 组1.已知,为不重合的两个平面,直线,那么“”是“”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件2.给出下列四个命题:①垂直于同一直线的两条直线 互相平行;②垂直于同一...