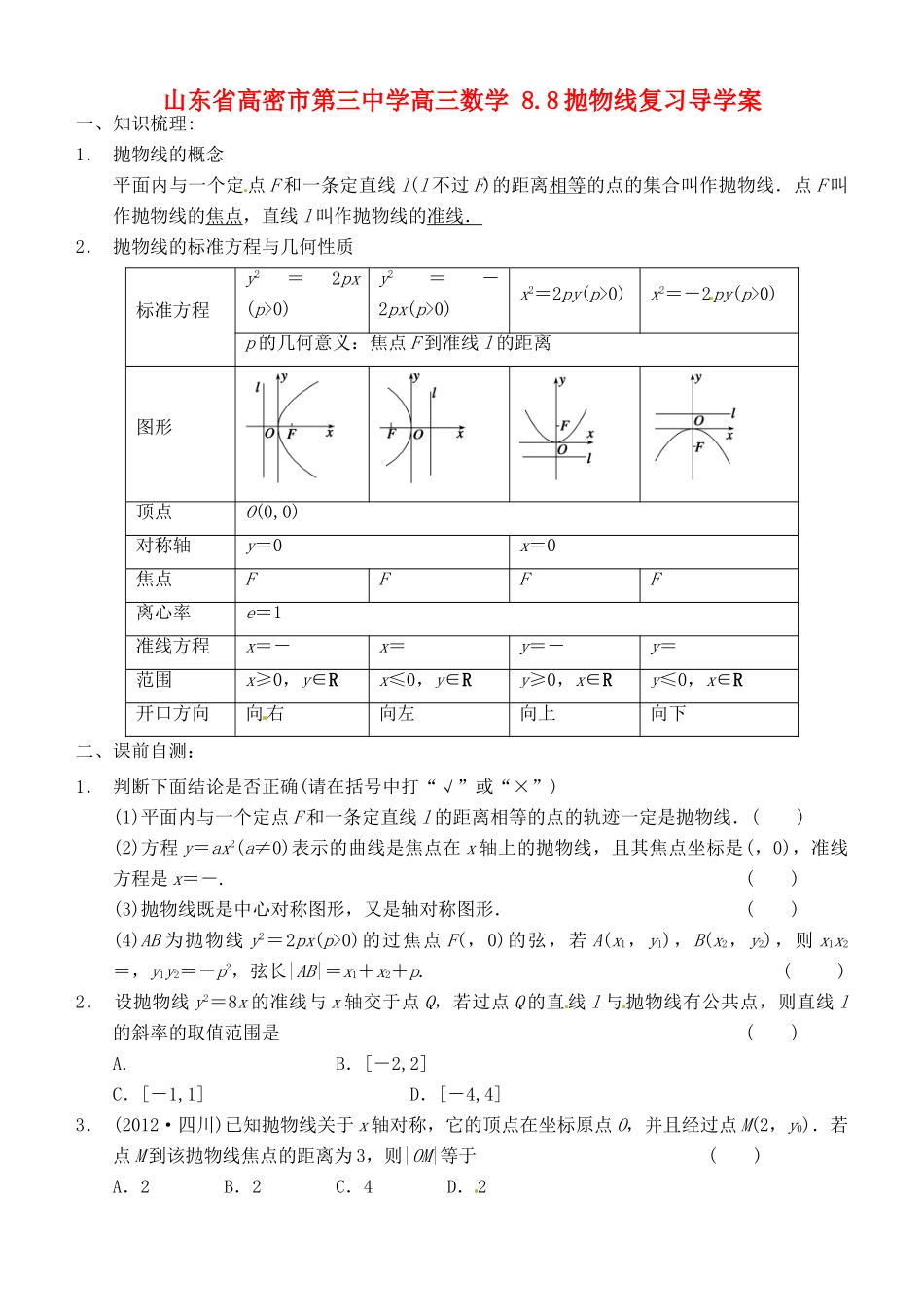
山东省高密市第三中学高三数学 8.8 抛物线复习导学案一、知识梳理: 1. 抛物线的概念平面内与一个定 点 F 和一条定直线 l(l 不过 F)的距离相等的点的集合叫作抛物线.点 F 叫作抛物线的焦点,直线 l 叫作抛物线的准线.2. 抛物线的标准方程与几何性质标准方程y2=2px (p>0)y2=-2px(p>0)x2=2py(p>0)x2=-2py(p>0)p 的几何意义:焦点 F 到准线 l 的距离图形顶点O(0,0)对称轴y=0x=0焦点FFFF离心率e=1准线方程x=-x=y=-y=范围x≥0,y∈Rx≤0,y∈Ry≥0,x∈Ry≤0,x∈R开口方向向右向左向上向下二、课前自测:1. 判断下面结论是否正确(请在括号中打“√”或“×”)(1)平面内与一个定点 F 和一条定直线 l 的距离相等的点的轨迹一定是抛物线.( )(2)方程 y=ax2(a≠0)表示的曲线是焦点在 x 轴上的抛物线,且其焦点坐标是(,0),准线方程是 x=-.( )(3)抛物线既是中心对称图形,又是轴对称图形.( )(4)AB 为抛物线 y2=2px(p>0)的过焦点 F(,0)的弦,若 A(x1,y1),B(x2,y2),则 x1x2=,y1y2=-p2,弦长|AB|=x1+x2+p.( )2. 设抛物线 y2=8x 的准线与 x 轴交于点 Q,若过点 Q 的直 线 l 与 抛物线有公共点,则直线 l的斜率的取值范围是( )A. B.[-2,2]C.[-1,1] D.[-4,4]3. (2012·四川)已知抛物线关于 x 轴对称,它的顶点在坐标原点 O,并且经过点 M(2,y0).若点 M 到该抛物线焦点的距离为 3,则|OM|等于( )A.2 B.2 C.4 D.24. 动圆过点(1,0),且与直线 x=-1 相切,则动圆的圆心的轨迹方程为__________.5. 若抛物线 y2=2px 的焦点与椭圆+=1 的右焦点重合,则 p 的值为________.三、典例分析:题型一 抛 物线的定义及应用例 1 已知抛物线 y2=2x 的焦点是 F,点 P 是抛物线上的动点,又有点 A(3,2),求|PA|+|PF|的最小 值,并求出取最小值时点 P 的坐标.跟踪练习:已知点 P 是抛物线 y2=2x 上的一个动点,则点 P 到点(0,2)的距离与点 P 到该抛物线准线的距离之和的最小值为( )A. B.3 C. D.题型二 抛物线的标准方程和几何性质例 2 抛物线的顶点在原点,对称轴为 y 轴,它与圆 x2+y2=9 相交,公共弦 MN 的长为 2,求该抛物线的方程,并写出它的焦点坐标与准线方程.跟踪训练 (1)设斜率为 2 的直线 l 过抛物线 y2=ax(a≠0)的焦点 F,且和 y 轴交于点 A.若△OAF(O 为坐标原点)的...