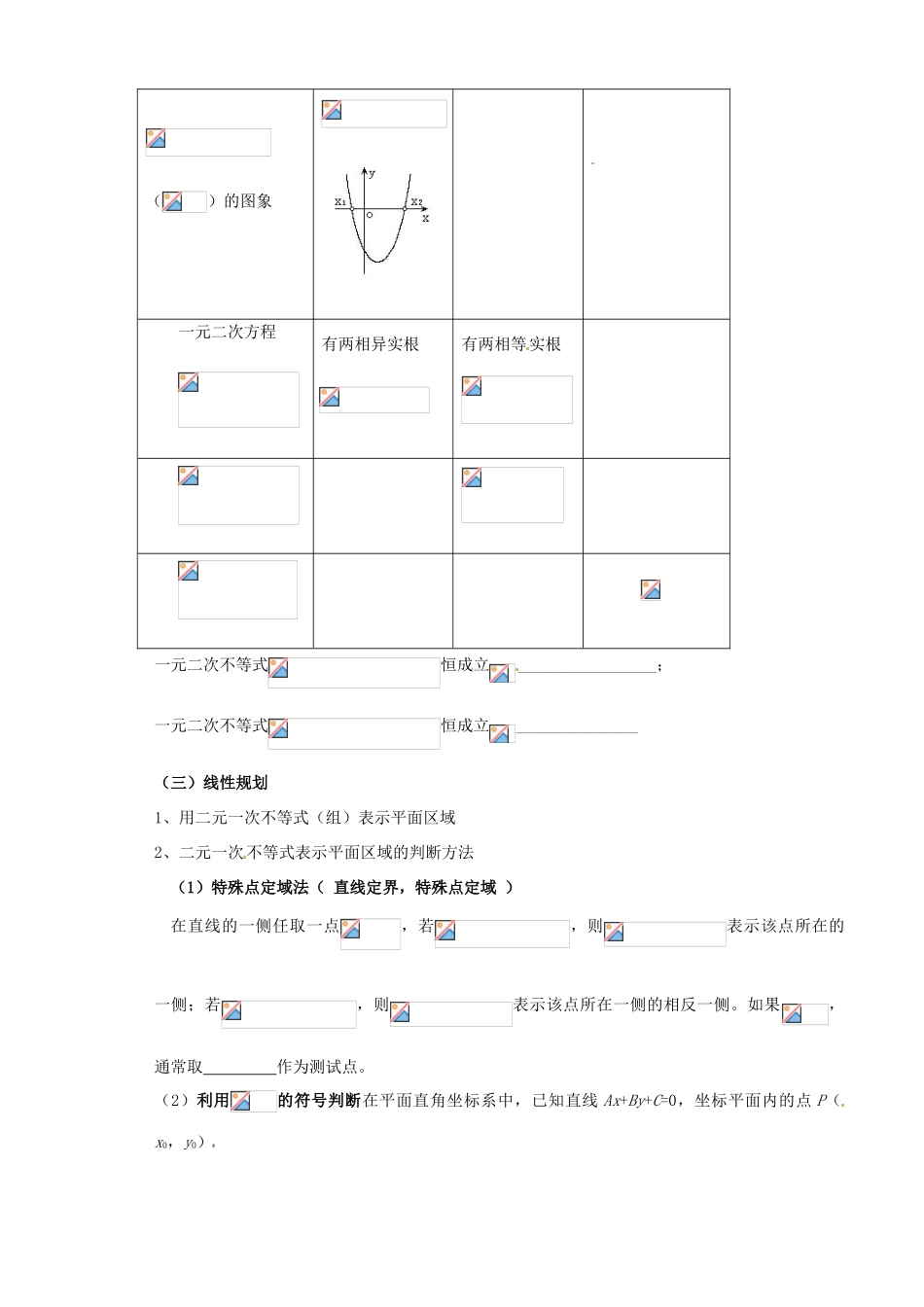
山西省原平市第一中学 2012-2013 学年高一数学 不等式小结学案1、应用不等式(组)表示不等关系;(一)不等式的主要性质:(1)对称性: ___________________________(2)传递性:_______________________________ (3)加法法则:________________________;_________________________ (4)乘法法则:________________________;__________________________ _____________________________(5)倒数法则:_______________________________(6)乘方法则:_______________________________(7)开方法则:_______________________________ 2、应用不等式的性质比较两个实数的大小;作差法3、应用不等式性质证明(二)一元二次不等式及其解法一元二次不等式的解集:设相应的一元二次方程的两根为,,则不等式的解的各种情况如下表: 二次函数()的图象一元二次方程有两相异实根有两相等实根 一元二次不等式恒成立_________________;一元二次不等式恒成立_______________(三)线性规划1、用二元一次不等式(组)表示平面区域2、二元一次不等式表示平面区域的判断方法(1)特殊点定域法( 直线定界,特殊点定域 )在直线的一侧任取一点,若,则表示该点所在的一侧;若,则表示该点所在一侧的相反一侧。如果,通常取 作为测试点。(2)利用的符号判断在平面直角坐标系中,已知直线 Ax+By+C=0,坐标平面内的点 P(x0,y0)新疆源头学子小屋特级教师王新敞http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/王新敞特级教师源头学子小屋新疆B>0 时,① Ax0+By0+C>0,则点 P(x0,y0)在直线的_____;② Ax0+By0+C<0,则点 P(x0,y0)在直线的______当 B<0 时 , ① Ax+By+C > 0 表 示 直 线 Ax+By+C=0____ 的 区 域 ; ② Ax+By+C < 0 表 示 直 线Ax+By+C=0_____的区域新疆源头学子小屋特级教师王新敞http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/王新敞特级教师源头学子小屋新疆3、线性规划的有关概念:可行域:_____________________线性规划问题的最优解:_____________________________________.4、求线性目标函数在线性约束条件下的最优解的步骤:(1)设变量,寻找线性约束条件,线性目标函数;(2)由二元一次不等式表示的平面区域做出可行域;(3)在可行域内求目标函数的最优解(四)基本不等式1、如果 a,b 是正数,那么2、基本不等式几何意义是_____________________________.例 1:比较与例 2:解不等式组:(1)(2)例 3:(1)画出下列不等式表示的区域(2)不等式表示的区域在直线的 ( )A. 右上方 B. 右下方 C. 左上方 D. 左下方例 4:若关于 x 的不等式的解集为,求 m 的值.例 5:已知函数(Ⅰ)当时,求函数的最小值;(Ⅱ)若对任意,恒成立,试求实数的取值范围.