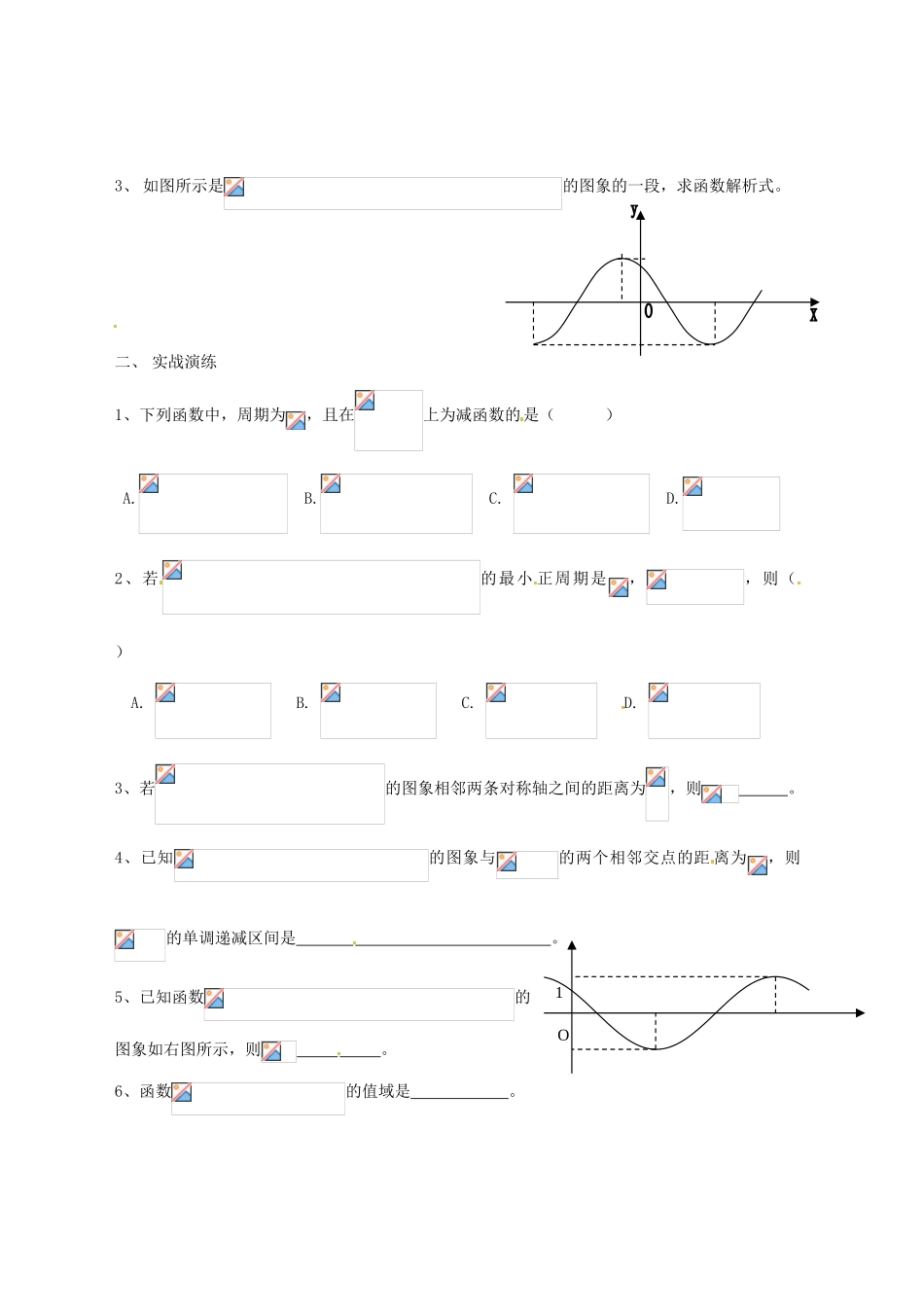
山西省原平市第一中学 2012-2013 学年高一数学 三角函数 复习与小结(二)导学案1、理解并熟练运用三角函数的图象和性质,会用数形结合思想解题;2、能够准确进行图象的变换,会读图并结合“五点法”确定的解析式;二、文本研读:复习回顾本章所学 1.4—1.6 内容,总结并回答下列问题1、 总结正弦、余弦、正切函数的图象与性质,完成下表:定义域值域简图]画法图象周期性奇偶性单调性最值对称轴对称中心2、 总结函数的图象的画法: ① 五点法:② 图象变换法:一、 知识应用1、 比较下列各组函数值的大小: ⑴.与; ⑵. 与 ; ⑶. 与2、 按要求完成问题,已知函数:⑴.利用“五点法”作出函数图象,并指出它的周期、频率、相位、初相、最值;⑵. 求函数的单调递减区间。⑶.叙述由的图象变换得到已知函数图象的过程(两种方法)。3、 如图所示是的图象的一段,求函数解析式。二、 实战演练1、下列函数中,周期为,且在上为减函数的是( ) A. B. C. D.2、若的最小 正周期是,,则( )A. B. C. D. 3、若的图象相邻两条对称轴之间的距离为,则 。4、已知的图象与的两个相邻交点的距 离为,则的单调递减区间是 。5、已知函数的图象如右图所示,则 。6、函数的值域是 。1O7、将的图象向右平移个单位后,得到的图象的对称中心是 。8、求函数的定义域、周期和单调区间。9、已知的图象与轴的交点中,相邻两个交点之间距离为,且图象上一个最低点 为, ⑴.求的解析式; ⑵.画出函数在区间上的图象。三、 能力提升1、 要得到的图象,需将的图象进行怎样的变换?2、 已知的最大值为,最小值为, ⑴.求的值; ⑵.求函数在上的值域。