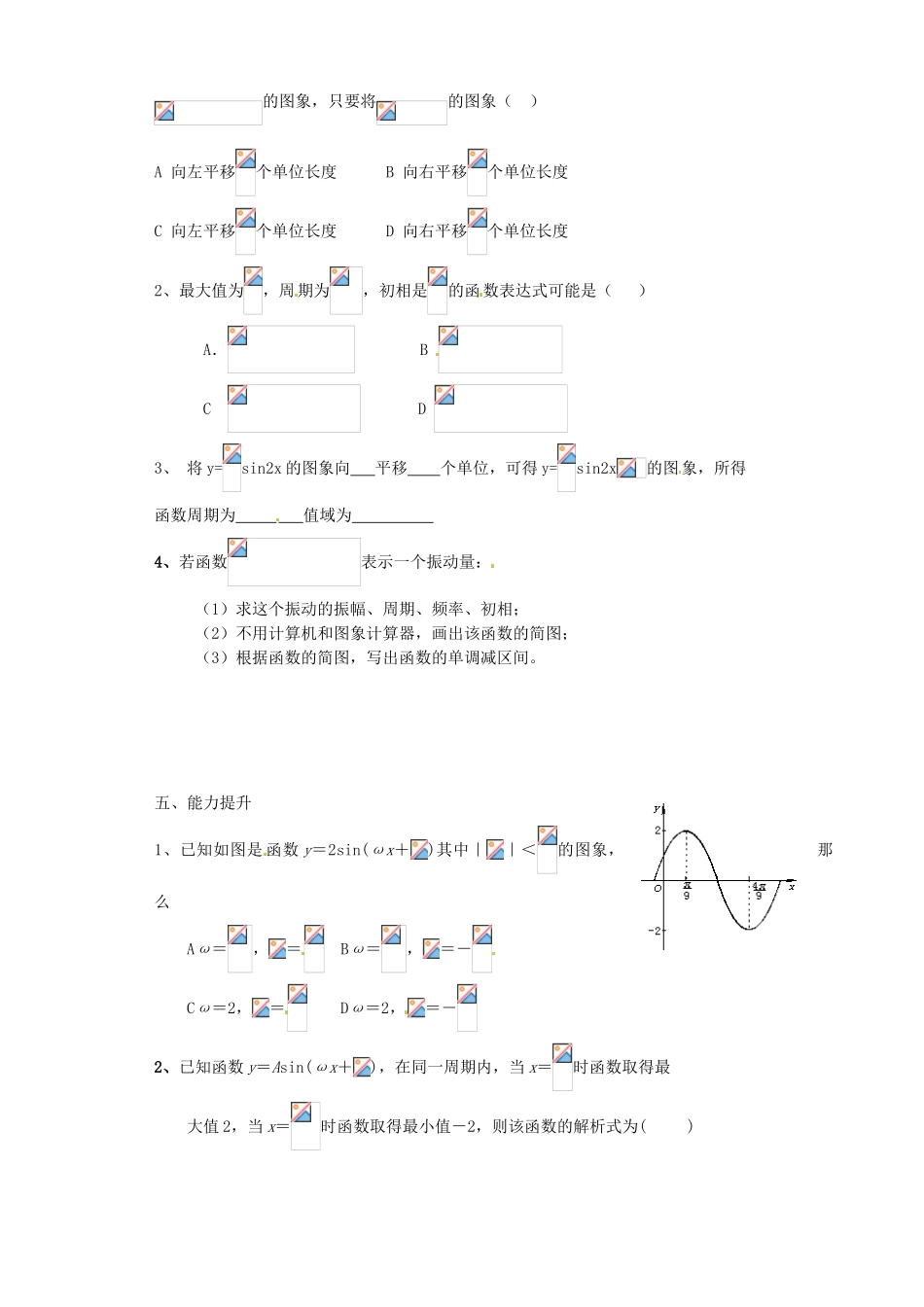
山西省原平市第一中学 2012-2013 学年高一数学 正弦函数图像 2 导学案学会用参数思想讨论变换过程,掌握图象变换 与函数解析式的内在联系的认识,会用五点法解题。二、文本研读阅读教材 P51—P52 探究(三)回答下列问题1、你阅读后把你知道的记下来,并展示给全班同学。2、请大家完成函数。 3、请你完成上节与本节内容的一般性结论。 4、完成 P53 例 3 并把方法写出来。5、阅读教材 P54 把你知道的记下来,并完成例 2三、知识应用1.已知简谐运动的图象经过点(0,1),则该简谐运动的最小正周期和初相分别为 、 .2. 函数在区间的简图是 。3、 将 y=sin2x 的图象向 平移 个单位,可得 y=sin2x的图象,所得函数周期为 值域为 4、将y=sinx 图象上各点的纵坐标变为原来的 ___ 且将各点的横坐标变为原来的 ______ 可得 y=3sinx 的图象.四、实战演练1 、 已 知 函 数的 最 小 正 周 期 为, 为 了 得 到 函 数A.B.C.D.的图象,只要将的图象( )A 向左平移个单位长度 B 向右平移个单位长度C 向左平移个单位长度 D 向右平移个单位长度 2、最大值为,周期为,初相是的函数表达式可能是( )A. B C D 3、 将 y=sin2x 的图象向 平移 个单位,可得 y=sin2x的图象,所得函数周期为 值域为 4、若函数表示一个振动量:(1)求这个振动的振幅、周期、频率、初相;(2)不用计算机和图象计算器,画出该函数的简图;(3)根据函数的简图,写出函数的单调减区间。五、能力提升1、已知如图是 函数 y=2sin(ωx+)其中||<的图象,那么Aω=,= Bω=,=-Cω=2,= Dω=2,=-2、已知函数 y=Asin(ωx+),在同一周期内,当 x=时函数取得最大值 2,当 x=时函数取得最小值-2,则该函数的解析式为( )Ay=2sin(3x-) By=2sin(3x+Cy=2sin(+) Dy=2sin(-)3、已知函数的图象经过点,试写出函数的一条对称轴方程为 .4、函数 f(x)=sin(ωx+φ)的图象交 x 轴于相邻的两点 A、B,A、B 的距离为 1, 图象过点(1,-),则 f(x)= .5、函 数的部分图象如图所示,(1)求的表达式;(2)指出可由怎样变换得到;(3)求关于直线对称函数的解析式.6、设函数,图象的一条对称轴是直线.(1)求;(2)求函数的单调增区间;(3)写出的对称中心与对称轴(4)画出函数在区间上的图象.六、归纳小结y4-46x10