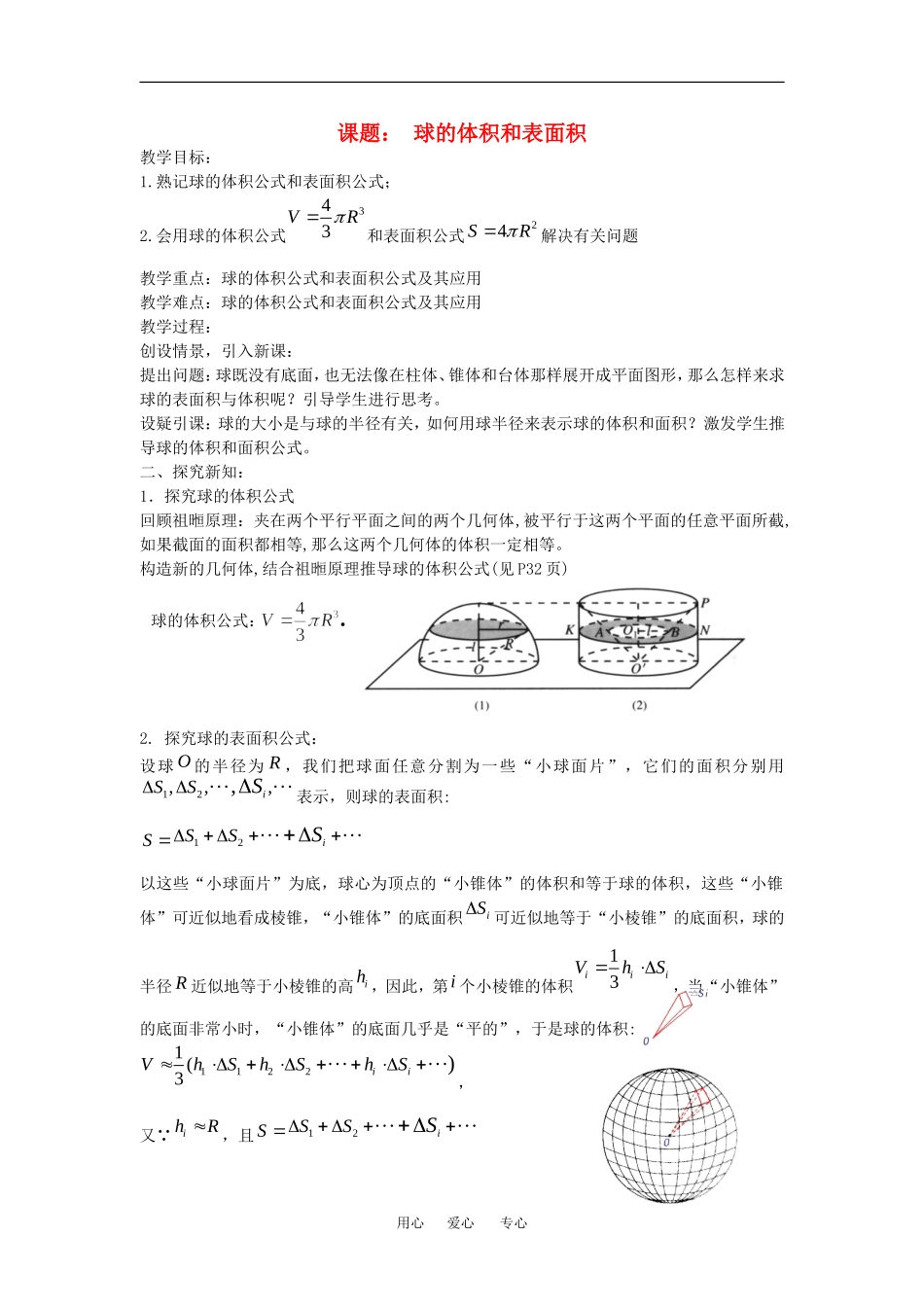
课题: 球的体积和表面积教学目标:1.熟记球的体积公式和表面积公式;2.会用球的体积公式343VR和表面积公式24SR解决有关问题教学重点:球的体积公式和表面积公式及其应用教学难点:球的体积公式和表面积公式及其应用教学过程:创设情景,引入新课:提出问题:球既没有底面,也无法像在柱体、锥体和台体那样展开成平面图形,那么怎样来求球的表面积与体积呢?引导学生进行思考。设疑引课:球的大小是与球的半径有关,如何用球半径来表示球的体积和面积?激发学生推导球的体积和面积公式。二、探究新知:1.探究球的体积公式回顾祖暅原理:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截面的面积都相等,那么这两个几何体的体积一定相等。构造新的几何体,结合祖暅原理推导球的体积公式(见 P32 页) 2. 探究球的表面积公式:设球 O 的半径为 R ,我们把球面任意分割为一些“小球面片”,它们的面积分别用12,,,,iSSS 表示,则球的表面积:S 12iSSS 以这些“小球面片”为底,球心为顶点的“小锥体”的体积和等于球的体积,这些“小锥体”可近似地看成棱锥,“小锥体”的底面积iS可近似地等于“小棱锥”的底面积,球的半径 R 近似地等于小棱锥的高ih ,因此,第i 个小棱锥的体积13iiiVhS,当“小锥体”的底面非常小时,“小锥体”的底面几乎是“平的”,于是球的体积:11221 (3)iiVhShShS,又 ihR,且 S 12iSSS 用心 爱心 专心球的体积公式:奎屯王新敞新疆RA'C'CAOA'B'C'D'DCBAOA'B'C'D'DCBAOA'C'CAO∴可得13VR S,又 343VR,∴13 R S343R,∴24SR即为球的表面积公式三、例题示范,巩固新知:例 1 已 知 过 球 面 上, ,A B C 三 点 的 截 面 和 球 心 的 距 离 为 球 半 径 的 一 半 , 且2ABBCCA ,求球的表面积解:设截面圆心为O,连结O A ,设球半径为 R ,则232 32323O A ,在 Rt O OA中,222OAO AO O,∴2222 31()34RR,∴43R ,∴26449SR.例 2.半球内有一个内接正方体,正方体的一个面在半球的底面圆内,若正方体棱长为6 ,求球的表面积和体积解:作轴截面如图所示,6CC,262 3AC ,设球半径为 R ,则222ROCCC 22( 6)( 3)9∴3R ,...