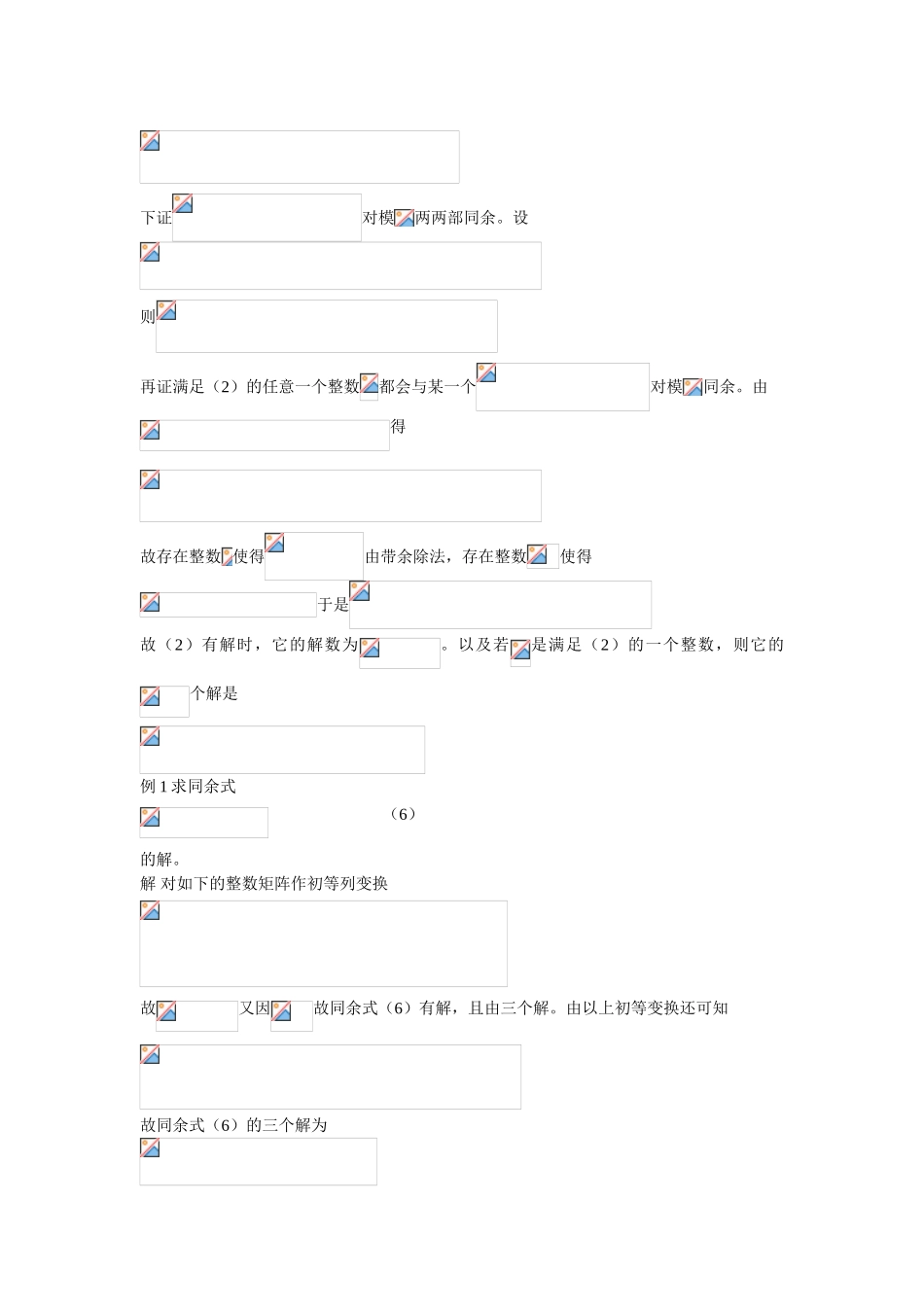
1 基本概念及一次同余式定义 设,其中是整数,又设,则 (1)叫做模的同余式。若,则叫做同余式(1)的次数。假如满足则叫做同余式(1)的解。不同余的解指互不同余的解。当及都比较小时,可以用验算法求解同余式。如例 1 同余式仅有解例 2 同余式有个解例 3 同余式无解。定理 一次同余式 (2)有解的充要条件是若(2)有解,则它的解数为。以及当同余式(2)有解时,若是满足(2)的一个整数,则它的个解是 (4)证 易知同余式(2)有解的充要条件是不定方程 (5)有解。而不定方程(5)有解的充要条件为当同余式(2)有解时,若是满足(2)的一个整数,则下证对模两两部同余。设则再证满足(2)的任意一个整数都会与某一个对模同余。由得故存在整数 使得由带余除法,存在整数使得于是故(2)有解时,它的解数为。以及若是满足(2)的一个整数,则它的个解是 例 1 求同余式 (6)的解。解 对如下的整数矩阵作初等列变换故又因故同余式(6)有解,且由三个解。由以上初等变换还可知故同余式(6)的三个解为即例 2 求同余式 (7)的解。解 对作辗转相除法。故同余式(7)有唯一解。由以上过程还可知故故同余式(7)的解为即 习题1.求下列同余式的解:(ⅰ) (ⅱ) (ⅲ)解(ⅰ)因故,于是该同余式有解,且对模 337 有唯一解。并且但是故于是该同余式的唯一解为(ⅱ)由辗转相除法,可得故该同余式有解.由辗转相除法,还可得在这个等式两边同时乘以 112,得故因故故该同余式的全部解为即2.求联立同余式的解。解 由同余式得代入同余式得对做辗转相除法。因故且故故由可得由及得于是可得,该联立同余式的解为3.(ⅰ)设是正整数,,证明是同余式的解。(ⅱ)设是质数,,证明是同余式的解。证(ⅰ)因是正整数,故同余式有唯一解。由欧拉定理得故是同余式的解。(ⅱ)因是质数,,故,同余式有惟一解。因,故易知而,故因此因,故于是因此,是同余式的解。