江苏省淮安中学高二数学《空间几何体的体积》学案二

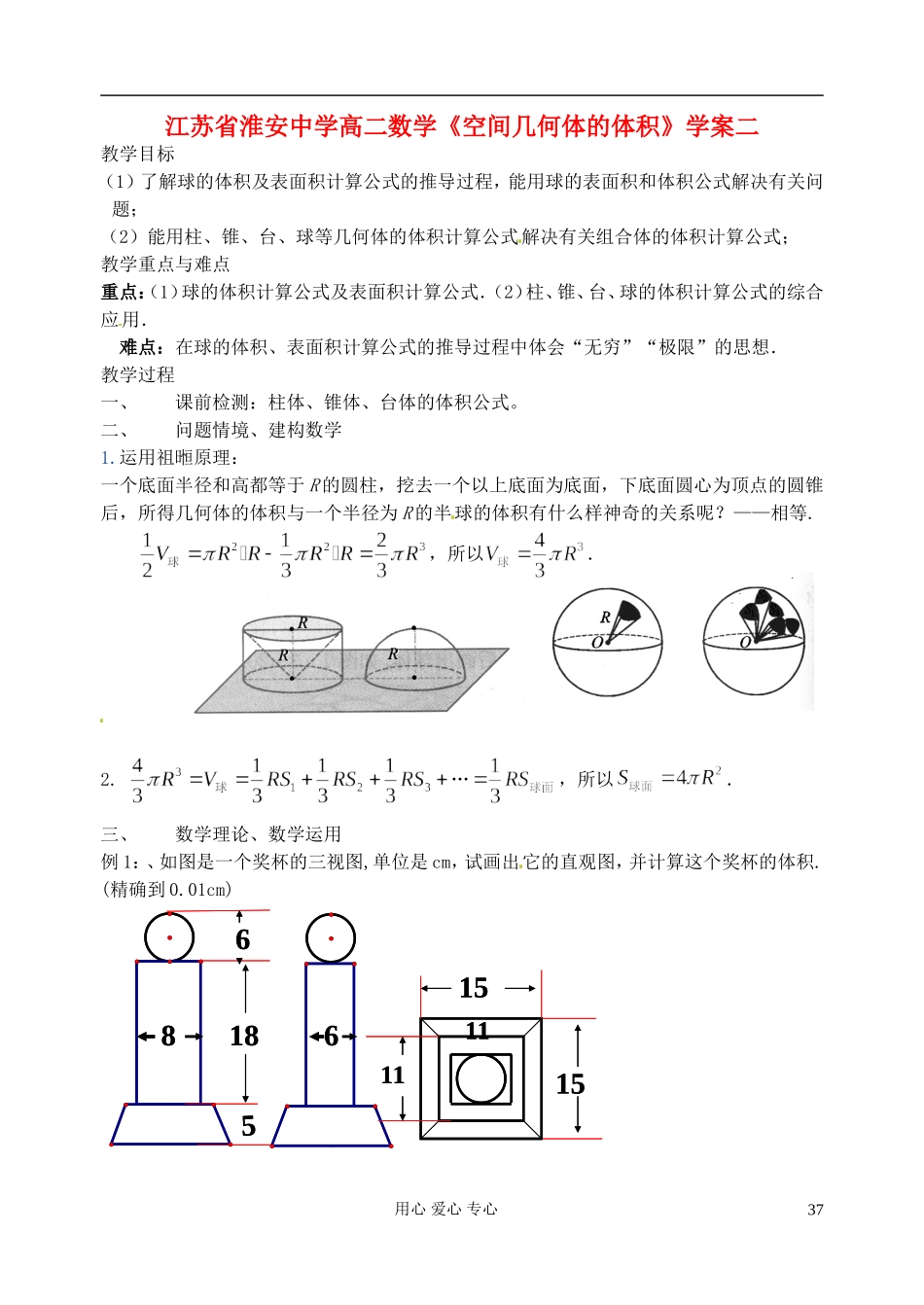
江苏省淮安中学高二数学《空间几何体的体积》学案二教学目标（1）了解球的体积及表面积计算公式的推导过程，能用球的表面积和体积公式解决有关问题；（2）能用柱、锥、台、球等几何体的体积计算公式解决有关组合体的体积计算公式；教学重点与难点重点：（1）球的体积计算公式及表面积计算公式．（2）柱、锥、台、球的体积计算公式的综合应用．难点：在球的体积、表面积计算公式的推导过程中体会“无穷”“极限”的思想．教学过程一、课前检测：柱体、锥体、台体的体积公式。二、问题情境、建构数学1.运用祖暅原理：一个底面半径和高都等于 R 的圆柱，挖去一个以上底面为底面，下底面圆心为顶点的圆锥后，所得几何体的体积与一个半径为 R 的半球的体积有什么样神奇的关系呢？——相等.，所以．2. …，所以．三、数学理论、数学运用例 1：、如图是一个奖杯的三视图,单位是 cm，试画出它的直观图，并计算这个奖杯的体积.(精确到 0.01cm)8661851515111186618515151111用心 爱心 专心37DCBAC1B1A1例 2、用刀切一个近似球体的西瓜，切下的较小部分的圆面直径为 30 cm，高度为 5 cm，该西瓜体积大约有多大? 例 3、正三棱柱中，是中点，，（1）求证： (2)求到平面的距离。例 4、把长、宽分别为 4、3 的矩形以一条对角线为痕折成直二面角，求过此四个顶点所在球的内接正方体的表面积和体积。 用心 爱心 专心38五、课堂小结：六、布置作业：1.3.2 空间几何体的体积（2）作业班级 姓名 学号 等第 1、已知高为 3 的直三棱柱 ABC—A1B1C1的底是边长为 1 的正三角形，则三棱锥 B1—ABC 的体积为 。2、一正方体和一圆柱等高，且侧面积也相等，试比较它们体积的大小_____________3、一平面截一球得到直径是 6cm 的圆面，球心到这个平面的距离是 4cm。则该球的体积是 cm3。4、若三个球的表面积之比为，则它们的体积之比为 5、棱长为 1 的正方体的外接球半径是 ；内切球半径是 6、棱长为 1 的正四面体外接球的半径为 7、表面积为324π 的球，其内接正四棱柱的高是 14，这个正四棱柱的表面积为 8、在长方体中，用截面截下一个棱锥，求的体积与剩余部分的体积比。用心 爱心 专心39D1C1B1A1DCBA9、设三棱柱的体积为 V，P，Q 分别是侧棱上的点，且，求四棱锥的体积10、如图，平面 ADE平面 ABCD，是边长为的等边三角形，是矩形，F 是 AB中点，EC 与平面成角，（1）求证：；（2）求四棱锥的体积;用心 爱心 专心40EABCDHF