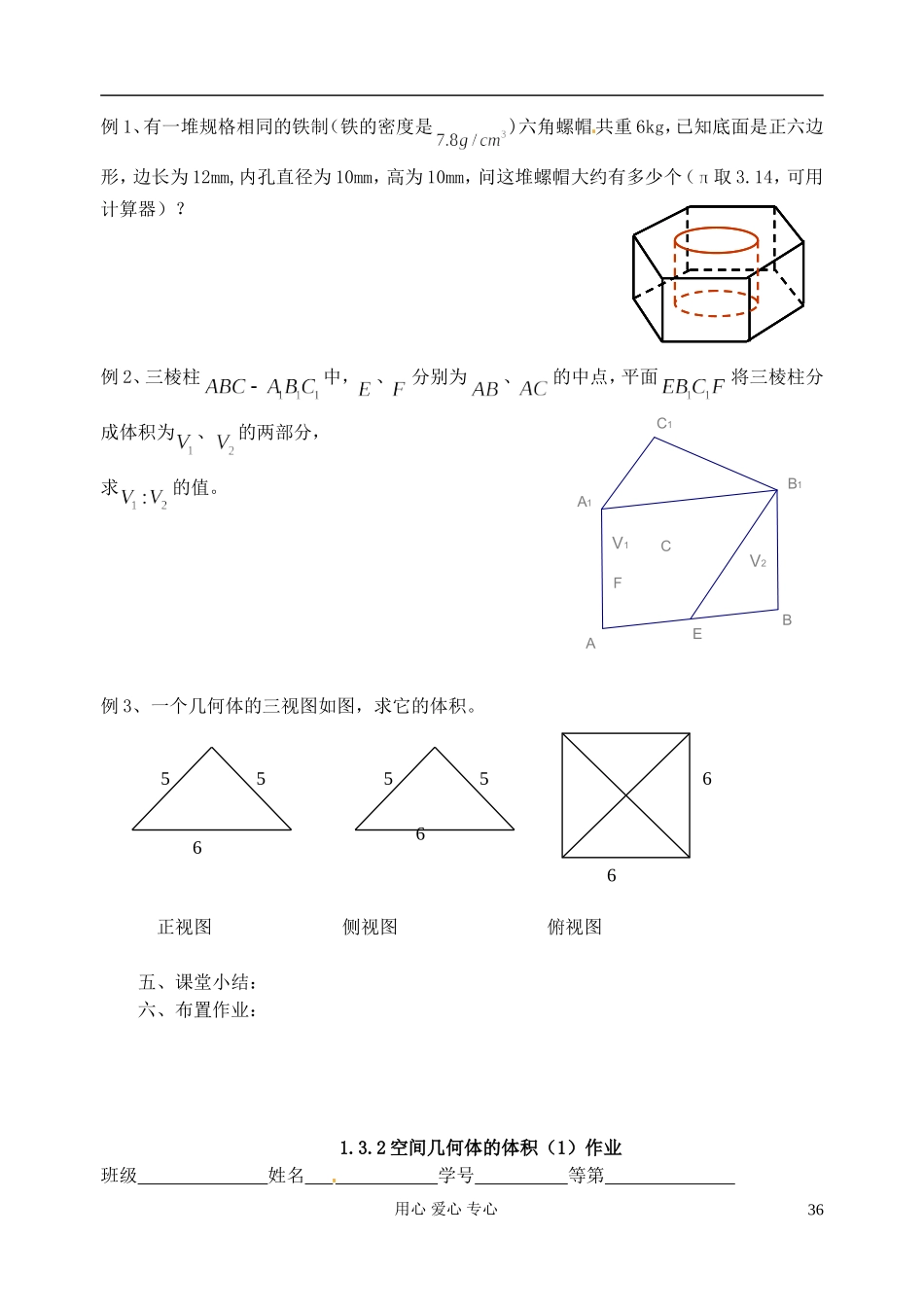
江苏省淮安中学高二数学《空间几何体的体积》学案一教学目标(1)了解柱、锥、台的体积公式,能运用公式求解有关体积计算问题;(2)了解柱体、锥体、台体空间结构的内在联系,感受它们体积之间的关系;(3)培养学生空见想象能力、理性思维能力以及观察能力.教学重点与难点重点:柱、锥、台的体积计算公式及其应用.难点:运用公式解决有关体积计算问题.教学过程一、课前检测:正棱柱、正棱锥、正棱台及圆柱、圆锥、圆台的侧面积公式。二、创设情境、引入新课在初中的学习中,我们已经会根据长方体的长、宽、高来计算长方体的体积,棱柱、棱锥、棱台以及圆柱、圆锥、圆台的体积如何计算?它们的体积计算公式之间有何联系?三、讲解新课1、 棱柱(圆柱)可由多边形(圆)沿某一方向平行得到,因此,两个底面积相等、高也相等的棱柱(圆柱)具有相等的体积。 柱体(棱柱、圆柱)的体积等于它的底面积和高的积,即 2、底面积相等,高也相等的两个锥体,它们的体积也相等3、台体(棱台、圆台)的体积可以转化为锥体的体积来计算,如果台体的上、下底面面积分别为,,高是,可以推得它的体积是 4、柱、锥、台体的体积公式之间的关系如下: 四、数学应用用心 爱心 专心35V1V2C1B1A1FCBEA例 1、有一堆规格相同的铁制(铁的密度是)六角螺帽共重 6kg,已知底面是正六边形,边长为 12mm,内孔直径为 10mm,高为 10mm,问这堆螺帽大约有多少个(取 3.14,可用计算器)?例 2、三棱柱中,、分别为、的中点,平面将三棱柱分成体积为、的两部分,求的值。例 3、一个几何体的三视图如图,求它的体积。正视图 侧视图 俯视图五、课堂小结:六、布置作业:1.3.2 空间几何体的体积(1)作业班级 姓名 学号 等第 用心 爱心 专心65565566361、正三棱锥的底面边长为 2,侧面均为直角三角形,则此三棱锥的体积为 2、正六棱台的两底面边长分别为和 2,高为,则它的体积为 3、已知两个平行于底面的平面将棱锥的高分成相等的三段,则此棱锥被分成三部分的体积(自上至下)之比为 4、已知正方体棱长为,三棱锥的体积为 5、正棱锥的高和底面边长都缩小为原来的时,它的体积是原来 6、一个空间几何体的正视图,侧视图,俯视图为全等的等腰直角三角形,直角边长为 1,则几何体的体积是 7、在中,,,(如图),若将绕直线旋转一周,求所成的旋转体的体积。8、若一个圆台下底面面积是上底面面积的 4 倍,高是 3,体积是 63,求圆台的侧面积...