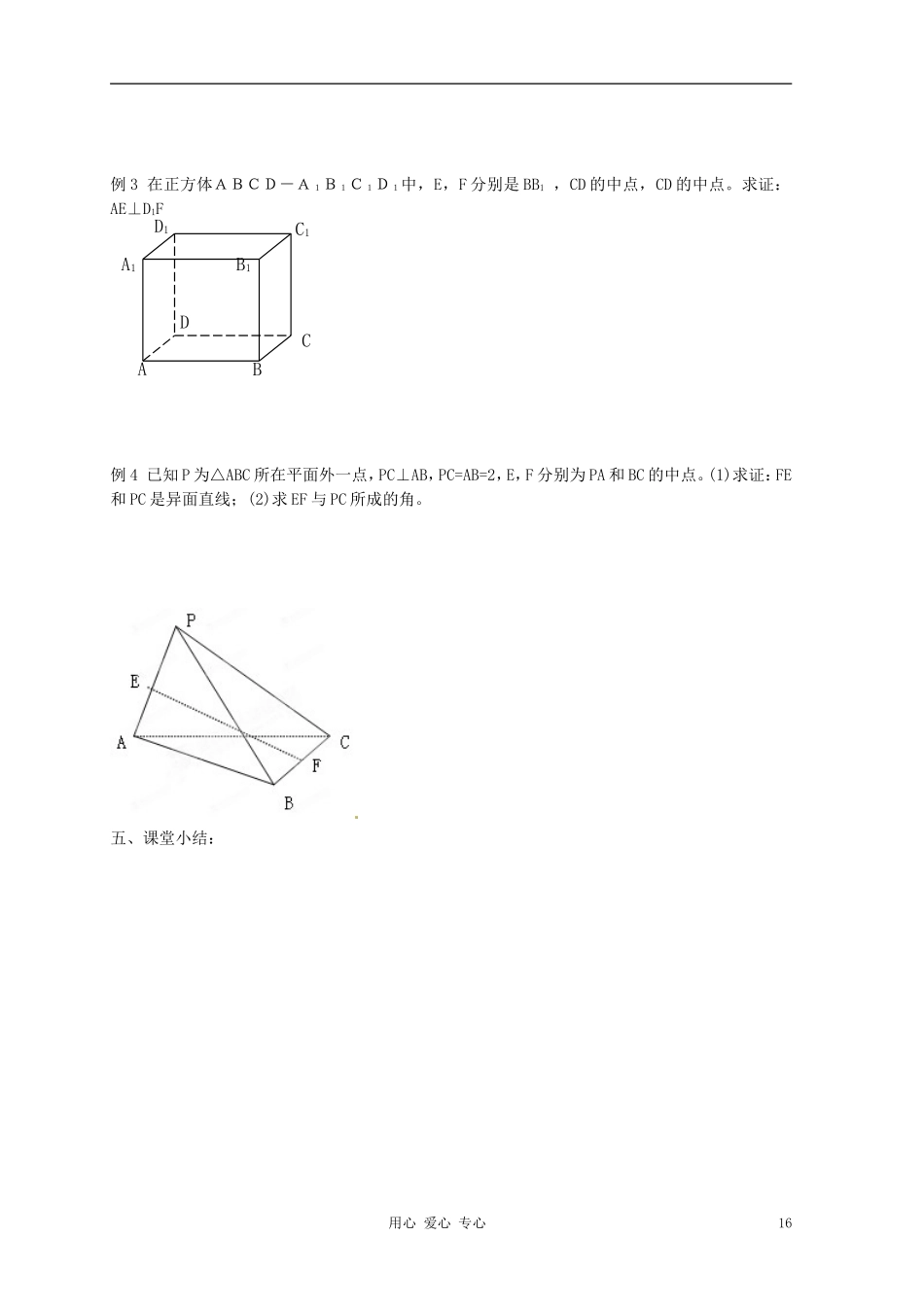
江苏省淮安中学高二数学《空间两直线的位置关系》学案二【教学目标】1、理解异面直线以及异面直线所成角的概念。 2、能根据异面直线所成的角的定义在具体图形中能初步识别并求出异面直线所成的角。 3、了解两直线相互垂直的定义。【教学重点】1、异面直线及异面直线所成角的概念的理解。 2、两条直线互为异面直线的判定依据的证明。3、异面直线所成角的判断与求解。【教学难点】异面直线所成角的判断与求解。【教学过程】课前检测:1、空间两条直线的位置关系有______、_______、________;也可以分为______、_________2、异面直线是指____________________________3、平行同一条直线的两条直线______,用符号表示为________________________4、如果一个角的两边和另一个角的两边分别平行,且方向相反,那么这两个角___一、问题情境 对于两条相交直线的具体位置,我们可以通过研究它们的夹角的大小来刻画它们的具体位置关系,在空间能否找到一个几何量来刻画两条异面直线的具体位置关系?二、学生活动 1、探索异面直线所成角的的定义。 2、探索异面直线所成角的步骤。 三、建构数学 1、异面直线所成角的定义______________________________________ 2、异面直线所成角的范围_____________________________________3、求异面直线所成角的步骤:___________________________________ ___________________________________ ___________________________________4、两异面直线相互垂直的定义_________________________________ 四、教学运用例 1 求证:过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线。(反证法)例 2 已知ABCD-A1B1C1D1是棱长为 a 的正方体。(1)正方体的哪些棱所在的直线与直线 BC1是异面直线?(2)求异面直线 AA1与 BC 所成的角;(3)求异面直线 BC1和 AC 所成的角。用心 爱心 专心15A1ABCD1C1B1D例 3 在正方体ABCD-A1B1C1D1中,E,F 分别是 BB1 ,CD 的中点,CD 的中点。求证:AE⊥D1F例 4 已知 P 为△ABC 所在平面外一点,PC⊥AB,PC=AB=2,E,F 分别为 PA 和 BC 的中点。(1)求证:FE和 PC 是异面直线;(2)求 EF 与 PC 所成的角。五、课堂小结:用心 爱心 专心16A1ABCD1C1B1D1.2.2 空间两直线的位置关系(2)作业 班级___________姓名_____________学号____________等第___________1、下面四个命题:分别在两个平面内的两...