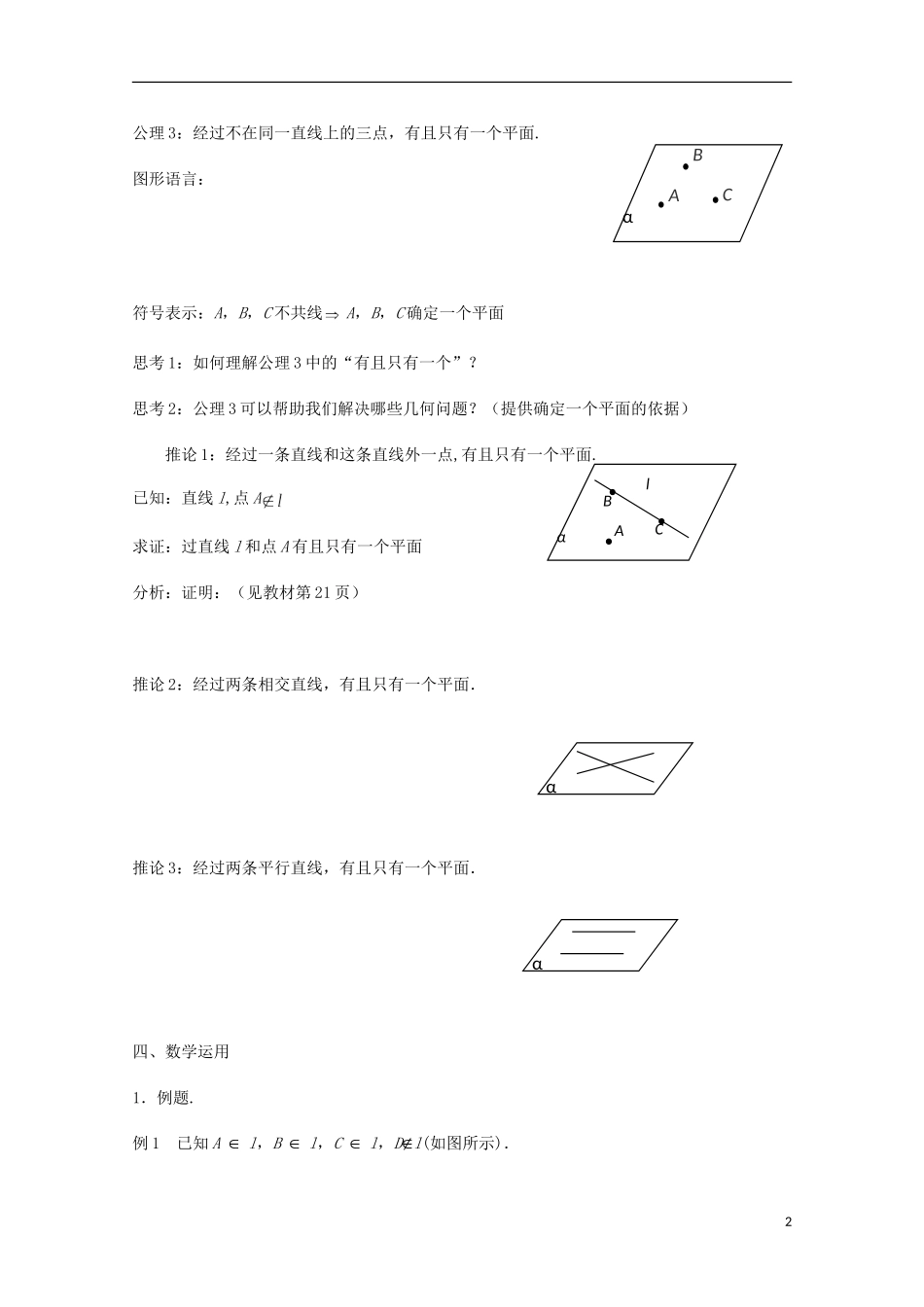
1.2.1 平面的基本性质(2)教学目标:掌握平面的基本性质的三条推论及作用.教材分析及教材内容的定位:本节内容是在上节中公理 3 的基础上进一步研究确定平面的条件,得出 3 条推论.对于推论的证明,是学生学习立体几何遇到的第一个需要论证的问题.教学时应注重分析证明的思路及论证的依据,并指出证明的过程,包括存在性与惟一性两部分.为学生运用符号语言证明几何问题提供示范,从而为后续学习打下基础.教学重点:平面性质的三条推论,注意它们的条件、结论、作用、图形语言及符号语言.教学难点:平面性质的三条推论的掌握与运用.教学方法:实验、探究、发现.教学过程:一、问题情境1.复习上节课学过的平面基本性质的两条公理及作用;2.问题:公理 1 可以理解为根据点与平面的关系确定直线与平面的位置关系,公理 2 可以理解为由点与平面的位置关系确定直线与平面的位置关系,如何确定一个平面呢?二、学生活动学生回顾思考并讨论问题;三、建构数学1公理 3:经过不在同一直线上的三点,有且只有一个平面.图形语言:符号表示:A,B,C 不共线A,B,C 确定一个平面思考 1:如何理解公理 3 中的“有且只有一个”?思考 2:公理 3 可以帮助我们解决哪些几何问题?(提供确定一个平面的依据)推论 1:经过一条直线和这条直线外一点,有且只有一个平面.已知:直线 l,点 A求证:过直线 l 和点 A 有且只有一个平面分析:证明:(见教材第 21 页)推论 2:经过两条相交直线,有且只有一个平面.推论 3:经过两条平行直线,有且只有一个平面.四、数学运用1.例题.例 1 已知 A Î l,B Î l,C Î l,DÏl(如图所示).2αBCAlαααCAB 求证:直线 AD,BD,CD 共面.变式练习:求证:两两相交且不共点的三条直线必在同一个平面内.例 2 如图,若直线 l 与四边形 ABCD 的三条边 AB,AD,CD 分别交于点 E,F,G.求证:四边形ABCD 为平面四边形.例 3 已知 a⊂a,b⊂a,a∩b=A,P Î a,PQ∥b.求证:PQ⊂a.2.练习.(1)判断下列命题是否正确.① 如果一条直线与两条直线都相交,那么这三条直线确定一个平面.② 经过一点的两条直线确定一个平面.③ 经过一点的三条直线确定一个平面.④ 平面和平面交于不共线的三点 A、B、C.(2)空间四点 A、B、C、D 共面但不共线,则下列结论成立的是______.① 四点中必有三点共线. ②四点中必有三点不共线.③AB、BC、CD、DA 四条直线中总...