江苏省白蒲中学2013高一数学 三角函数教案25 苏教版

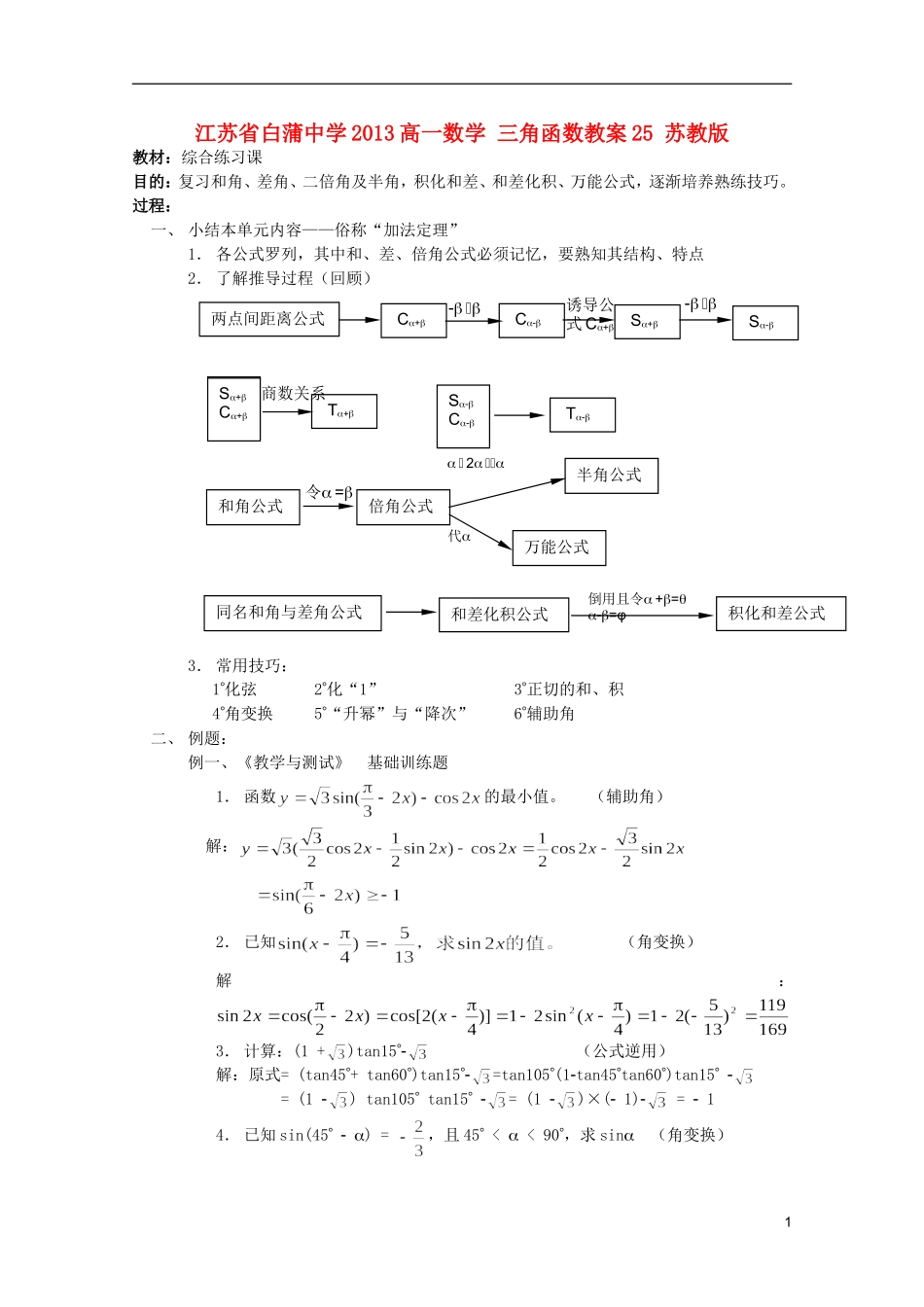
江苏省白蒲中学 2013 高一数学 三角函数教案 25 苏教版教材：综合练习课 目的：复习和角、差角、二倍角及半角，积化和差、和差化积、万能公式，逐渐培养熟练技巧。过程：一、 小结本单元内容——俗称“加法定理”1． 各公式罗列，其中和、差、倍角公式必须记忆，要熟知其结构、特点2． 了解推导过程（回顾）3． 常用技巧： 1化弦 2化“1” 3正切的和、积 4角变换 5“升幂”与“降次” 6辅助角二、 例题：例一、《教学与测试》 基础训练题1． 函数的最小值。 （辅助角） 解： 2． 已知 （角变换） 解：3． 计算：(1 +)tan15 （公式逆用）解：原式= (tan45+ tan60)tan15=tan105(1tan45tan60)tan15  = (1 ) tan105 tan15 = (1 )×( 1) =  14． 已知 sin(45  ) = ，且 45 <  < 90，求 sin （角变换）1两点间距离公式 C+ C S+ SS+C+ T+S+C+SC T和角公式倍角公式半角公式万能公式同名和角与差角公式和差化积公式积化和差公式 代 代诱导公式 C+商数关系令 = 代 2 代代代倒用且令 +==φ解：∵45 <  < 90 ∴45 < 45 < 0 ∴cos(45) = cos2 = sin(902) = sin[2(45)] = 2sin(45)cos(45) =即 1  sin2 = ， 解之得：sin = 例二、已知是三角形中的一个最小的内角， 且，求 a 的取值范围解：原式变形： 即，显然 （若，则 0 = 2） ∴ 又∵，∴ 即： 解之得：例三、试求函数的最大值和最小值。 若呢？ 解：1．设 则 ∴ ∴ ∴ 2．若，则，∴ 即例四、已知 tan = 3tan( + )，，求 sin(2 + )的值。 解：由题设： 即 sin cos( + ) = 3sin( + )cos 即 sin( + ) cos + cos( + )sin = 2sin cos( + )  2cossin( + ) ∴sin(2 + ) = 2sin 又∵ ∴sin ∴sin(2 + ) = 1三、作业：《教学与测试》P117—118 余下部分2