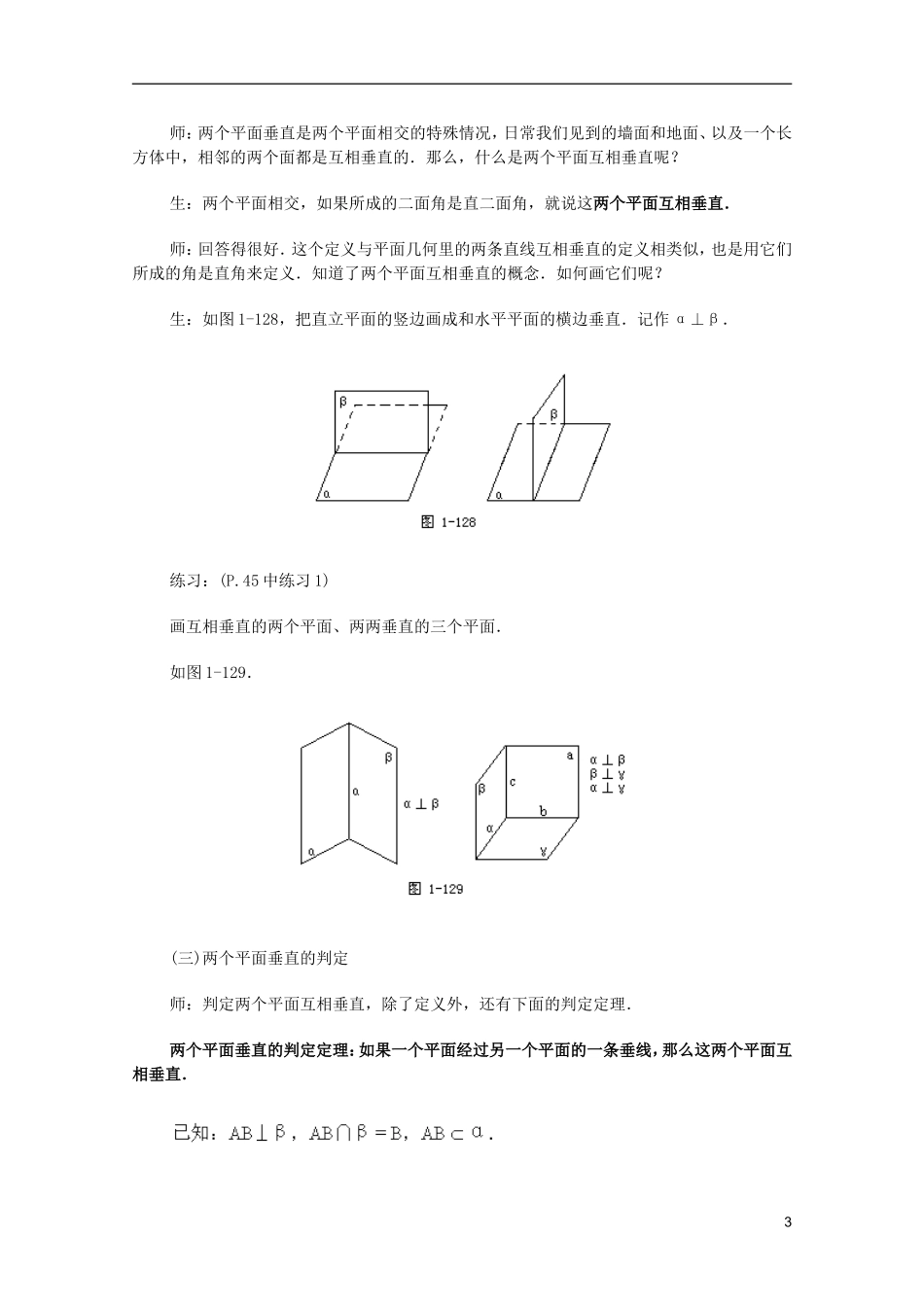
两个平面垂直的判定和性质(一) 一、素质教育目标(一)知识教学点1.两个平面垂直的定义、画法.2.两个平面垂直的判定定理.(二)能力训练点1.应用演绎的数学方法理解并掌握两个平面垂直的定义.2.掌握两个平面垂直的判定定理的证明过程,培养学生严格的逻辑推理,增强学生分析、解决问题的能力.3.利用转化的方法掌握和应用两个平面垂直的判定定理.(三)德育渗透点1.理解并掌握两个平面垂直定义的过程是培养学生从一般到特殊的思维方法的过程.2.让学生认识到掌握两个平面垂直的判定定理是人类生产实践的需要,并且应用于实践,进一步培养学生理论与实践相结合的观点.二、教学重点、难点、疑点及解决方法1.教学重点:掌握两个平面垂直的判定.2.教学难点:掌握两个平面垂直的判定及应用.三、课时安排本课题安排 2 课时.本节课为第一课时:主要讲解两个平面垂直的判定.四、教与学的过程设计(一)复习平面角的有关知识师:什么是二面角的平面角?生:以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角.1师:一般地,作二面角的平面角有哪几种方法?生:三种.一是利用定义;二是利用三垂线(逆)定理;三是利用棱的垂面.师:下面我们来做道练习(幻灯显示).已知:二面角 α-AB-β 等于 45°,CD<α,D∈AB,∠CDB=45°.求:CD 与平面 β 所成的角.生证明:作 CO⊥β 交 β 于点 O,连结 DO,则∠CDO 为 DC 与 β 所成的角.过点 O 作 OE⊥AB 于 E,连结 CE,则 CE⊥AB,∴∠CEO 为二面角 α-AB-β 的平面角,即∠CEO=45°. CO⊥OE,OC=OE,∴∠CDO=30°.即 DC 与 β 成 30°角.师点评:本题涉及到直线与平面所成角的范围[0°,90°]以及利用三垂线定理寻找二面角的平面角.事实上,利用三垂线定理作二面角的平面角是最常用,也是最有效的一种方法.(二)两个平面垂直的定义、画法2师:两个平面垂直是两个平面相交的特殊情况,日常我们见到的墙面和地面、以及一个长方体中,相邻的两个面都是互相垂直的.那么,什么是两个平面互相垂直呢?生:两个平面相交,如果所成的二面角是直二面角,就说这两个平面互相垂直.师:回答得很好.这个定义与平面几何里的两条直线互相垂直的定义相类似,也是用它们所成的角是直角来定义.知道了两个平面互相垂直的概念.如何画它们呢?生:如图 1-128,把直立平面的竖边画成和水平平面的横边垂直.记作...