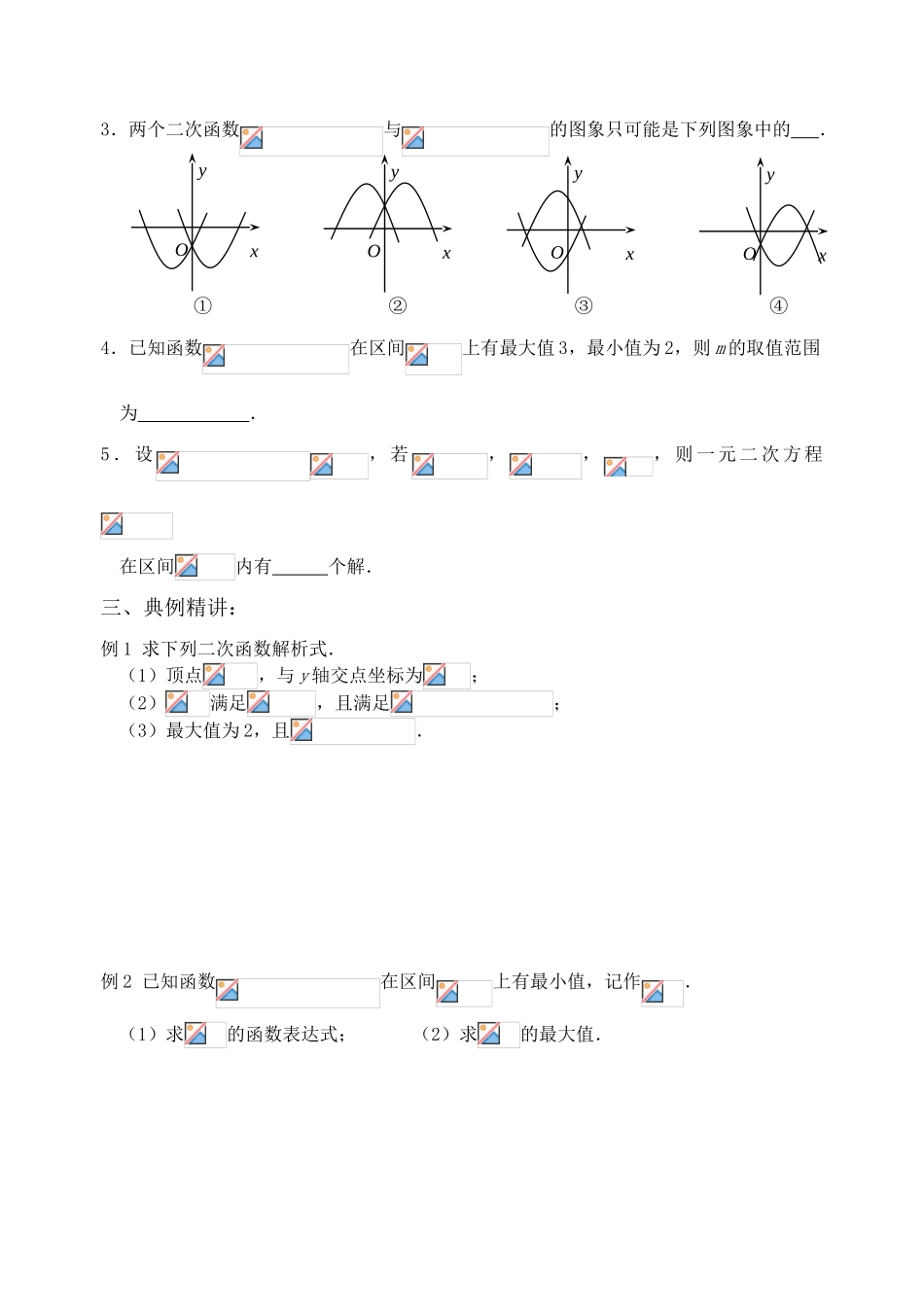
二次函数一、高考考纲要求:函数与方程 B,一元二次不等式 C.二、 复习目标 掌握二次函数的解析式的三种形式以及二次函数的图象和性质。三、重点难点: 二次函数的图象及性质四、要点梳理: 1 二次函数的解析式的三种形式 (1)一般式: (2)顶点式: (3)两根式: 2 二次函数的图象和性质 二次函数的图象是一条 ,对称轴方程为 ,顶点坐标为 (1)当时,抛物线开口向 ,函数在 上是单调减函数,在 上是单调增函数,当时,(2)当时,抛物线开口向 ,函数在 上是单调减函数,在 上是单调增函数,当时,五、基础自测:1.若二次函数,则其图象的开口向 ;对称轴方程为 ,顶点坐标为 ,与 x 轴的交点坐标为 ,最小值为 .2.如果二次函数的图象的对称轴为,那么 ,顶点坐标为 ,递增区间为 ,递减区间为 .3.两个二次函数与的图象只可能是下列图象中的 . ① ② ③ ④4.已知函数在区间上有最大值 3,最小值为 2,则 m 的取值范围为 .5 . 设, 若,,, 则 一 元 二 次 方 程在区间内有 个解.三、典例精讲:例 1 求下列二次函数解析式. (1)顶点,与 y 轴交点坐标为; (2)满足,且满足; (3)最大值为 2,且.例 2 已知函数在区间上有最小值,记作. (1)求的函数表达式; (2)求的最大值.OxyOxyOxyOxy例 3(1)已知方程在上有解,求 m 的取值范围;(2)已知关于 x 的二次方程有两个负根,求实数 k 的取值范围;(3)不等式对任意恒成立,求 a 的取值范围.七 反思感悟:八 千思百练:1.函数的零点为 .2 . 已 知是 偶 函 数 , 且, 则的 解 集 为 . 3 已知对于任意的,函数总大于零,则的范围 .4.已知,函数恒负,则的取值范围是 .5 二次函数的图象顶点为,且图象在轴上截得的线段长为 8,则这个二次函数的解析式为 .(必修 1 p93)6 已知是实数,函数若函数在区间上有零点,则的范围 7 设函数 的最大值为,则对于一切,的最大值为 8 设二次函数满足且的两实数根平方和为 10,图象过点(0,3),求的解析式。9 m 取何实数时,关于 x 的方程有实数解?10 已知函数(a,b 为实数),. (1)若,且函数的值域为,求的表达式; (2)在(1)的条件下,当时,是单调函数,求实数 k 的取值范围; (3)设,,,且为偶函数,判断能否大于零?