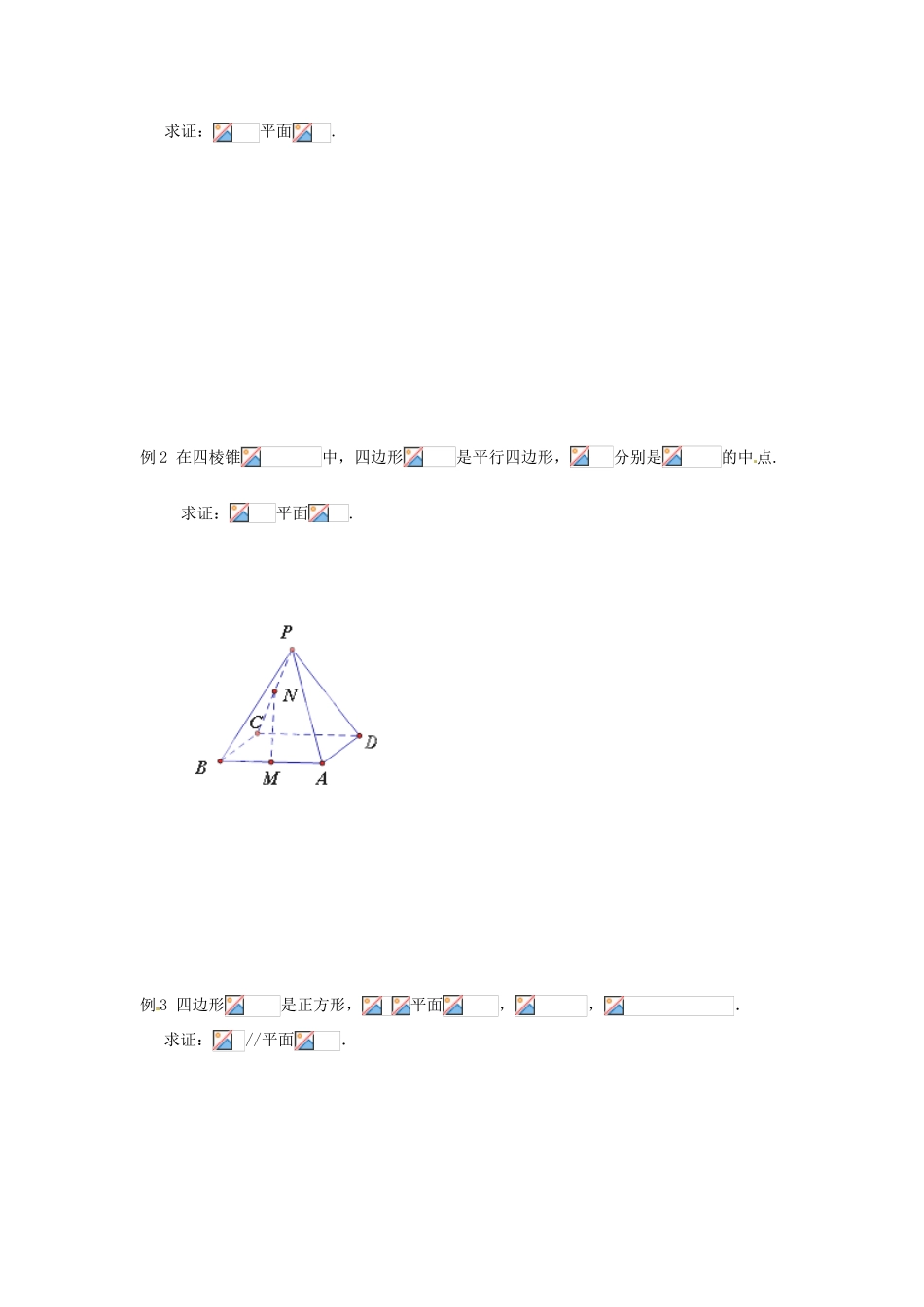
江苏省泰兴市第三高级中学 2014 届高三数学 直线与平面的位置关系复习导学案(艺术生)【基础知识】1、直线与平面平行的判定① 定义: .②判定定理: .即若,,,则 ③ 面面平行的定义: ,即若, ,则.2、直线与平面平行的性质定理如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交, 那么这条直线和 平行.【基本训练】1.若直线平面,则下列命题中正确的是____________.① 平行于内的所有直线; ② 平行于内的唯一确定的直线;③ 平行于任一条平行于的直线; ④ 平行于过 的平面与的交线.2.下列说法正确的是 . ① 直线 平行与平面内的无数条直线,则 //; ②若直线在平面外,则//; ③ 若直线,直线,则; ④ 若直线,,那么直线就平行于平面内的无数条直线.3.直线平面,直线,则与的关系是__________.4.已知是直线,是平面,给出下列命题中真命题有_______________.① 若,,则;②若,,则; ③若,,则;④ 若与异面,且,则与相交;⑤若与异面,则至多有一条直线与都垂直. 【典型例题讲练】例 1 四边形均为平行四边形,分别为对角线的中点.求证:平面. 例 2 在四棱锥中,四边形是平行四边形,分别是的中点.求证:平面. 例 3 四边形是正方形,平面,,.求证://平面.例 4 如图所示,在正方体中,是棱的中点.在棱上是否存在一点,使平面?证明你的结论.39 直线与平面的位置关系(2)【基础知识】1、直线与平面垂直的判定① 定义: .② 线面垂直的判定: .即若,,, , ,则.③ 如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于同一平面.即若,,则.④ 面面平行的性质: ,即若, ,则.2、直线和平面垂直的性质① 直线垂直于平面,则垂直于平面内________直线.②垂直于同一个平面的两条直线________.③ 垂直于同一直线的两个平面________.【基本训练】1.“直线与平面内无数条直线垂直”是“直线与平面垂直”的___________ 条件.2 .均 为 直 线 ,在 平 面内 , 则 “” 是的 条件.3.若是互不相同的空间直线, 是不重合的平面,则下列命题中为真命题的是_____ ___.① 若则 ②若则 ③ 若则; ④若,则.4.正方体中,与垂直的平面是________.① 平面; ②平面; ③平面; ④平面.【典型例题讲练】例 1 如图,为⊙的直径,为⊙上一点,平面,于,于.求证:平面.例 2 如图,在正方体中,是的中点,是底面正方形的中心...