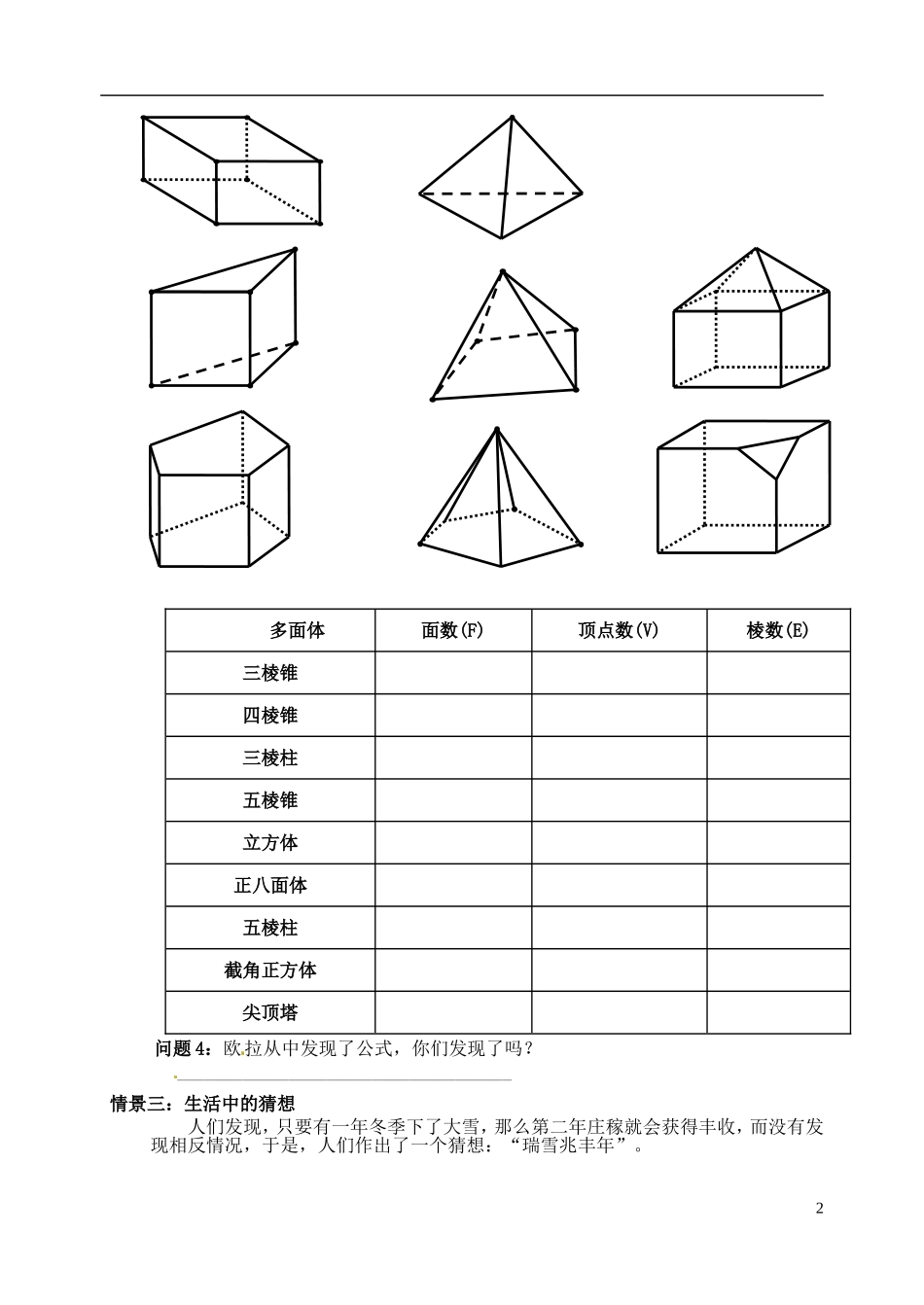
江苏省泰兴市第三高级中学高二数学 基于问题的合情推理导学案1 理教学目标:体会归纳推理这种基本的分析问题法,并把它们用于对问题的发现;明确归纳推理的一般步骤,并把这些方法用于实际问题的解决中去。正确认识归纳推理在数学中的重要作用,养成从小开始认真观察事物、分析问题、发现事物之间的质的联系的良好个性品质,善于发现问题,探求新知识教学重点:理解归纳推理的思维过程与一般形式。教学难点:运用归纳推理得到一般性的结论。教学过程:创设情境引入新课情景一:歌德巴赫猜想问题 1:同学们,你们有没有听说过一个世纪难题,歌德巴赫猜想,简称“1+1”? ____________________________________________问题 2:你们知道这个歌德巴赫猜想的具体内容吗? ____________________________________________问题 3:你们想不想知道歌德巴赫是怎样提出这个猜想的? 1742 年,歌德巴赫在教学中发现: 4=2+2, 6=3+3, 8=3+5, 10=3+7=5+5, 12=5+7, 14=3+11=7+7, 16=3+13=5+11, 18=5+13=7+11, 20=3+17=7+13, 22=3+19=5+17=11+11,…… 由此,他猜想:任何大于 2 的偶数都可以表示为两个素数之和(简称“1+1”),可是他既证明不了这个猜想,也否定不了这个猜想。于是,歌德巴赫写信给当时的大数学家欧拉。欧拉在给他的回信中说,他相信这个猜想是正确的,但他不能证明。叙述如此简单的问题,连欧拉这样首屈一指的数学家都不能证明,这个猜想便引起了许多数学家的注意。从提出这个猜想至今,许多数学家都不断努力想攻克它,但都没有成功。从此,这道著名的数学难题引起了世界上成千上万数学家的注意。200 年过去了,没有人证明它。哥德巴赫猜想由此成为数学皇冠上一颗可望不可及的“明珠”。到了 20 世纪 20 年代,才有人开始向它靠近。目前最佳的结果是中国数学家陈景润于 1966 年证明的“每一个充分大的偶数都能够表示为一个素数及一个不超过两个素数的乘积之和”(简称“1+2”),这一结论十分接近歌德巴赫猜想的解,被国际上称为“陈氏定理”。情景二:多面体的欧拉公式 虽然,歌德巴赫的猜想还不能证明,但他的这种猜想方法在定理发现中很有用。大数学家欧拉,也是通过观察一些简单的多面体,然后发现多面体的欧拉公式的。 下面请同学们数一数下列图中的凸多面体的面数 F、顶点数 V 和棱数 E,然后一起把表格填完整。1多面体面数(F)顶点数(V)棱数(E)三棱锥四棱锥三棱柱五棱锥立方体正八面体...