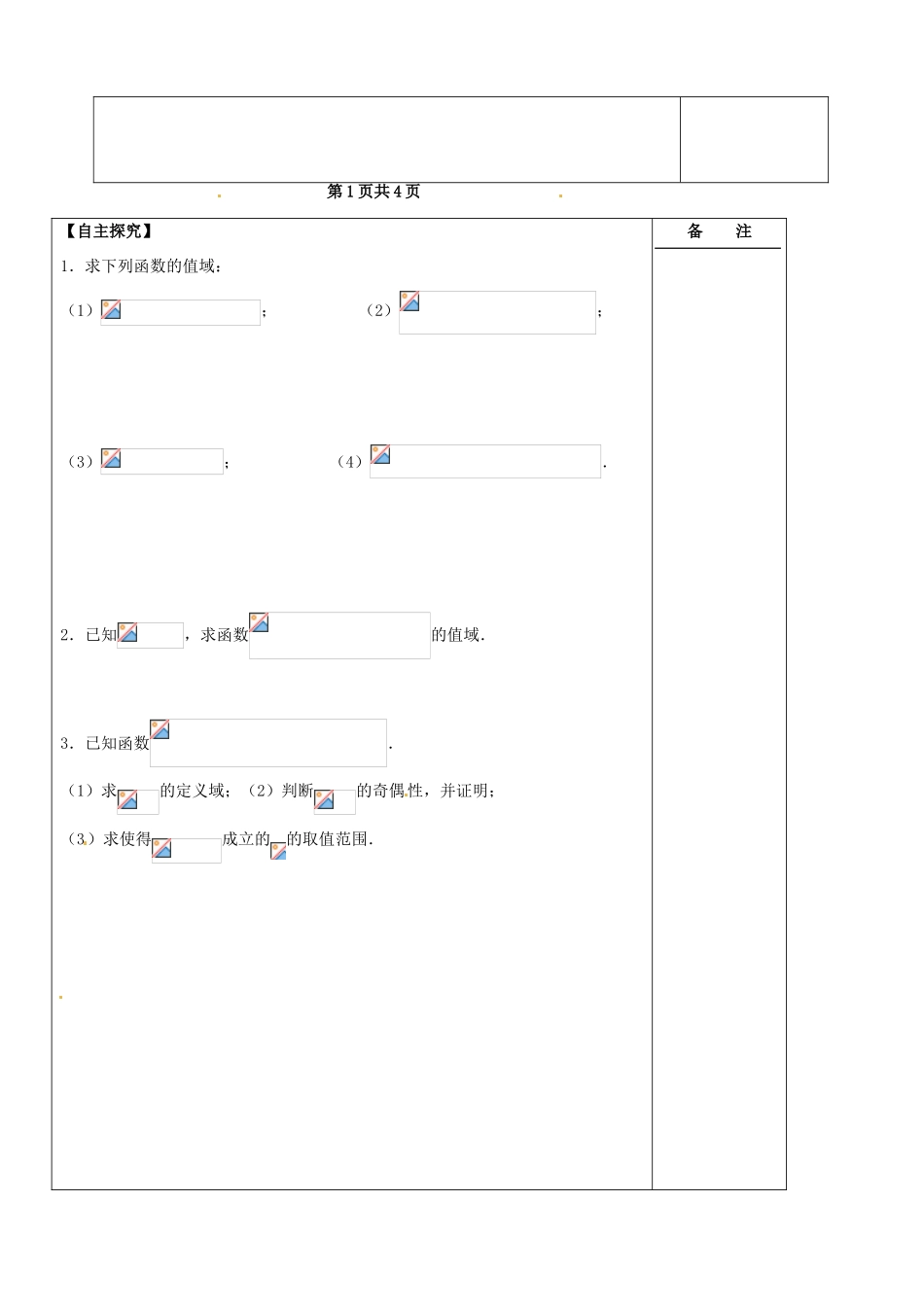
对数函数【学习目标】了解对数函数模型的实际案例;了解对数函数的概念;理解对数函数的性质,会画对数函数的图像.【问题情境】一、知识回顾:二、预习练习:1.函数的图像恒过定点_________.2.函数的定义域为_____________.3.若是奇函数,则实数=_________.4.比较下列数的大小:(1)_____;(2)_____;(3)_____;(4)_____;(5)______;(6)______.【我的疑问】备 注 第 1 页共 4 页 【自主探究】1.求下列函数的值域:(1); (2);(3); (4).2.已知,求函数的值域.3.已知函数.(1)求的定义域;(2)判断的奇偶性,并证明;(3)求使得成立的的取值范围.备 注第 2 页共 4 页【课堂检测】1.若的图像不经过第一象限,则的取值范围是_______.2.函数的值域是__________.3.解不等式的解集:(1);(2);(3).4.设,且,求的最小值.【回标反馈】备 注 第 3 页共 4 页 【巩固练习】1.函数是奇函数,则的解集为_______ ______.2.函数的图像恒过点,若点在直线上(其中),则的最小值为_________.3.对任意非零实数,恒有.(1)求的值;(2)求证是偶函数;(3)已知为区间上的增函数,解不等式.备 注