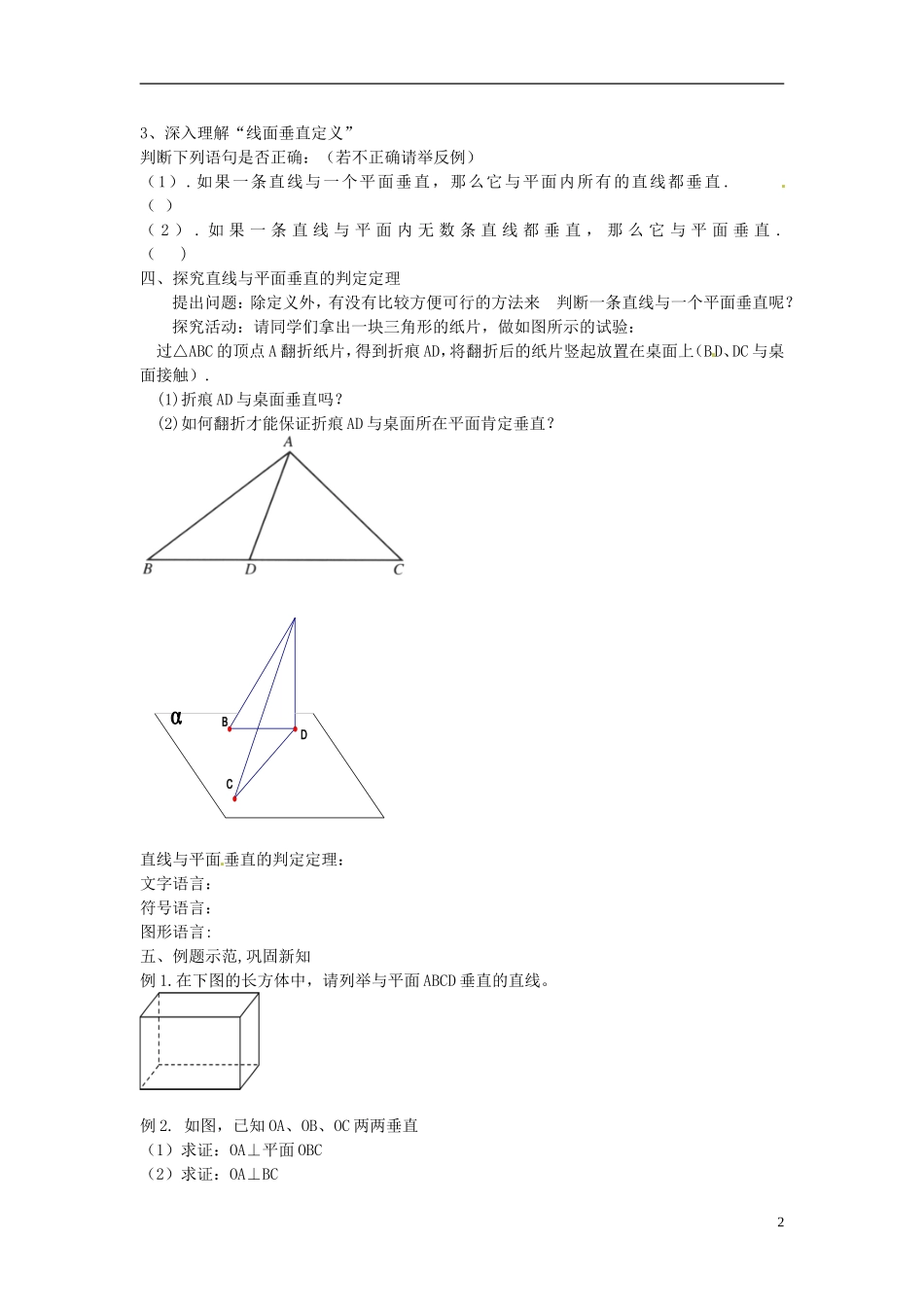
河南省濮阳市综合高中 2013-2014 学年高中数学必修 2 教案:直线与平面垂直教学目标:1、理解直线与平面垂直的定义;2、探究并归纳直线与平面垂直的判定定理;3、掌握直线与平面垂直的判定定理的应用。教学重点与难点:重点:对直线与平面垂直的判定定理的理解及应用。难点:直线与平面垂直的判定定理的应用教学过程一、复习回顾空间中直线与平面的位置关系有几种?1、直线在平面内;2、直线与平面平行;3、直线与平面相交(垂直)。二、探究直线与平面垂直的概念 1、举例说说生活中直线与平面垂直的现象(1)学校教学楼的柱子给人以直线与平面垂直的现象;(2)旗杆与地面的关系给人以直线与平面垂直的现象。2、问题:(1)如图,在阳光下观察直立于地面旗杆 AB 及它在地面的影子 BC,旗杆所在的直线与影子所在直线位置关系是什么?(2)旗杆 AB 与地面上任意一条不过旗杆底部 B 的直线 a 的位置关系又是什么?由以上探究可得到以下结论:AB 所在直线垂直于地面内过点 B 的直线AB 所在直线垂直于地面内不过点 B 的直线AB 所在直线垂直于地面内任意一条直线从而得到直线与平面垂直的定义。三、自主学习 建构新知1、阅读课本 p64 完成下列各题:直线与平面垂直的定义的(1)文字表示:(2)图形表示:(3)符号表示:2、直线 l 与平面 α 垂直的画法:通常地直线画成与表示平面的平行四边形的一边垂直。13、深入理解“线面垂直定义”判断下列语句是否正确:(若不正确请举反例)(1).如果一条直线与一个平面垂直,那么它与平面内所有的直线都垂直 . ( )( 2 ) . 如 果 一 条 直 线 与 平 面 内 无 数 条 直 线 都 垂 直 , 那 么 它 与 平 面 垂 直 . ( )四、探究直线与平面垂直的判定定理 提出问题:除定义外,有没有比较方便可行的方法来 判断一条直线与一个平面垂直呢?探究活动:请同学们拿出一块三角形的纸片,做如图所示的试验: 过△ABC 的顶点 A 翻折纸片,得到折痕 AD,将翻折后的纸片竖起放置在桌面上(BD、DC 与桌面接触). (1)折痕 AD 与桌面垂直吗? (2)如何翻折才能保证折痕 AD 与桌面所在平面肯定垂直?DBACBDC直线与平面垂直的判定定理:文字语言:符号语言:图形语言:五、例题示范,巩固新知例 1.在下图的长方体中,请列举与平面 ABCD 垂直的直线。例 2. 如图,已知 OA、OB、OC 两两垂直(1)求证:OA⊥平面 OBC(2)求证:OA⊥BC2...