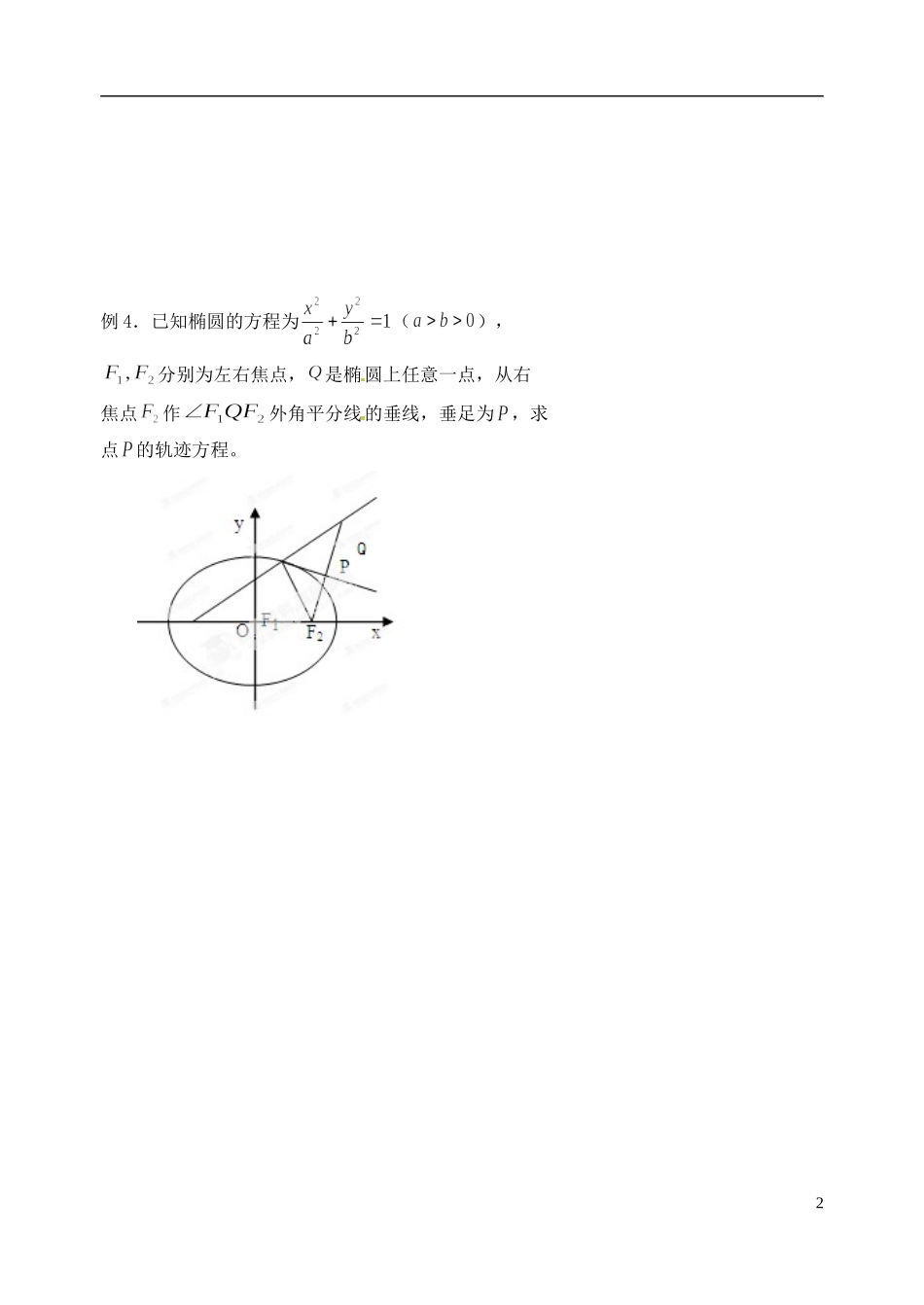
浙江省富阳二中高二数学上学期 利用定义解圆锥曲线中问题学案 新人教 A 版一.求值问题例 1:已知椭圆的方程为(),分别为左右焦点,P 是椭圆上任意一点(1)三角形的周长是多少?(2)三角形的面积何时最大?最大值是多少?(3)试讨论角为直角时点 P 的个数二.最值问题例 2、(1)抛物线 C:y2=4x 上一点 P 到点 A(3,4)与到准线的距离和最小,则点 P 的坐标为______________ (2)抛物线 C: y2=4x 上一点 Q 到点 B(4,1)与到焦点 F 的距离和最小,则点 Q 的坐标为 。(3)F 是椭圆的右焦点,A(1,1)为椭圆内一定点,P 为椭圆上一动点。则的最小值为 (4)定长为 3 的线段 AB 的两个端点在 y=x2上移动,AB 中点为 M,求点 M 到 x 轴的最短距离。三.轨迹问题例 3(1)动圆 M 与圆 C1:(x+1)2+y2=36 内切,与圆 C2:(x-1)2+y2=4 外切,求圆心 M 的轨迹方程。(2)一动圆与圆:外切,同时与圆:内切,求动圆圆心的轨迹方程,并说明它是什么样的曲线。(3)已知圆:,动圆与圆外切,且与直线相切,求动点的轨迹方程,并说明它是什么样的曲线。1例 4.已知椭圆的方程为(),分别为左右焦点,是椭圆上任意一点,从右焦点作外角平分线的垂线,垂足为,求点的轨迹方程。21、已知:F1,F2是双曲线的左、右焦点,过 F1作直线交双曲线左支于点 A、B,若,△ABF2的周长为( )A、4a B、4a+m C、4a+2m D、4a-m 2、若点 P 到点 F(4,0)的距离比它到直线 x+5=0 的距离小 1,则 P 点的轨迹方程是 ( )A、y2=-16x B、y2=-32x C、y2=16x D、y2=32x3、已知△ABC 的三边 AB、BC、AC 的长依次成等差数列,且,点 B、C 的坐标分别为(-1,0),(1,0),则顶点 A 的轨迹方程是( )A、 B、 C、 D、4、过原点的椭圆的一个焦点为 F(1,0),其长轴长为 4,则椭圆中心的轨迹方程是 ( )A、 B、C、 D、5、已知双曲线上一点 M 的横坐标为 4,则点 M 到左焦点的距离是 6、抛物线 y=2x2截一组斜率为 2 的平行直线,所得弦中点的轨迹方程是 7、已知抛物线 y2=2x 的弦 AB 所在直线过定点 p(-2,0),则弦 AB 中点的轨迹方程是 8、过双曲线 x2-y2=4 的焦点且平行于虚轴的弦长为 9、直线 y=kx+1 与双曲线 x2-y2=1 的交点个数只有一个,则 k= 10.F 是双曲线的右焦点,A(1,1)为一定点,P 为双曲线上上一动点,则的最小值为 11、设点 P 是椭圆上的动点,F1,F2是椭圆的...