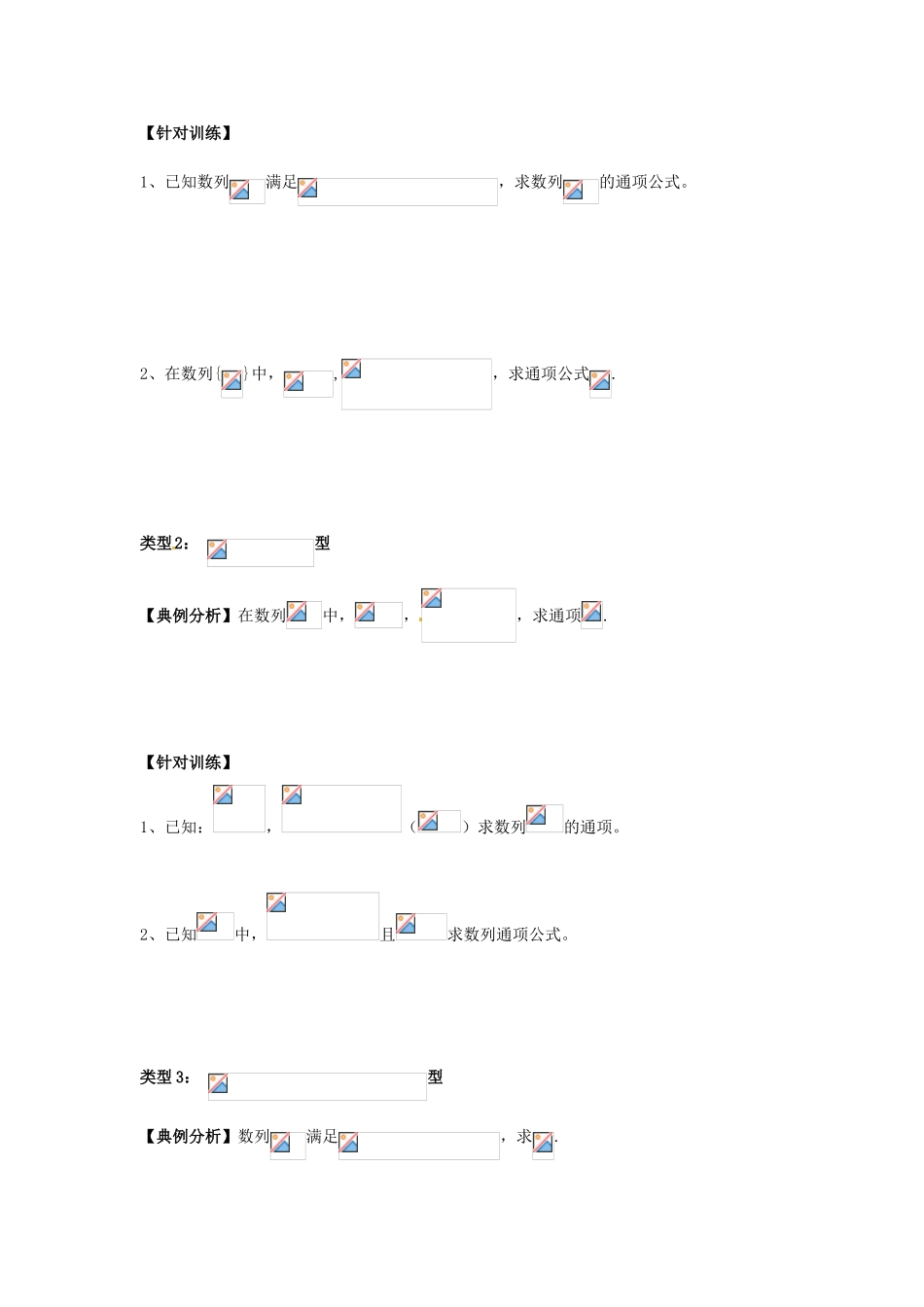
湖南省湘潭凤凰中学高三数学 数列复习学案 文数列的通项公式的定义: 如果数列{}的第 n项与 之间的关系可以用一个公式=f(n)来表示,那么这个公式叫做这个数列的通项公式.【考点集训】1.数列 1,,,,,…的一个通项公式 an是( ) A. B. C. D.2.数列,,2,…,则 2 是该数列的 ( )A.第 6 项 B.第 7 项 C.第 10 项 D.第 11 项3.下列说法正确的是( )A.数列 1,3,5,7 可表示为{1,3,5,7}B.数列 1,0,-1,-2 与数列-2,-1,0,1 是相同数列C.数列{}的第 k 项为 1+D.数列 0,2,4,6,…可记为{2n}4.下列关于星星的图案构成一个数列,该数列的一个通项公式是( ) A.an=n2-n+1 B.an= C.an= D.an=5.数列,,,,…中,有序数对(a,b)可以是__________.6.数列-1,7,-13,19,…的一个通项公式= 。7.数列 0,1,0,1,…的一个通项公式= 。类型 1: 型【典例分析】在数列中,且,求通项.【针对训练】1、已知数列满足,求数列的通项公式。2、在数列{}中,,,求通项公式.类型2: 型【典例分析】在数列中,,,求通项.【针对训练】1、已知:,()求数列的通项。2、已知中,且求数列通项公式。类型 3: 型【典例分析】数列满足,求.【针对训练】 1、已知满足,求通项公式。2、已知中,,()求。类型 4:型【典例分析】1、已知数列满足,且,求通项【针对训练】 已知:,时,,求的通项公式。【典例分析】2、已知数列满足(1)证明:数列是等差数列数列; (2)求数列的通项公式。【针对训练】已知数列满足,,求数列的通项公式。【变式训练】在数列中,.(1)设,求数列的通项公式;(2)求数列的前项的和.类型 5、取倒数【典例分析】已知数列{}中,其中,且当 n≥2 时,,求通项公式。【针对训练】1、数列中,且,,求数列的通项公式.2、,求3、在数列中,求. 类型 6、取对数法 【典例分析】 在数列中,,, 求. 【针对训练】若数列{}中,=3 且(n 是正整数),则它的通项公式是=▁▁▁【课后检测】1、已知数列{an}中,a1=2,an+1=an+n,则 a7为( )A.8 B.12 C.23 D.292、已知数列{an}中,a1=2,an=-(n≥2),则 a2 011等于 .3、数列{an}中,若 an+1=,a1=1,则 a6= 4、由下列数列的递推关系式求数列{an}的通项. (1)a 1=1,an=an-1+3n-1(n≥2); (2)a1=1,an=an-1(n≥2);(3), (4)a1=1,an+1=an+1.