高考数学 专项强化训练(六)试题VIP免费

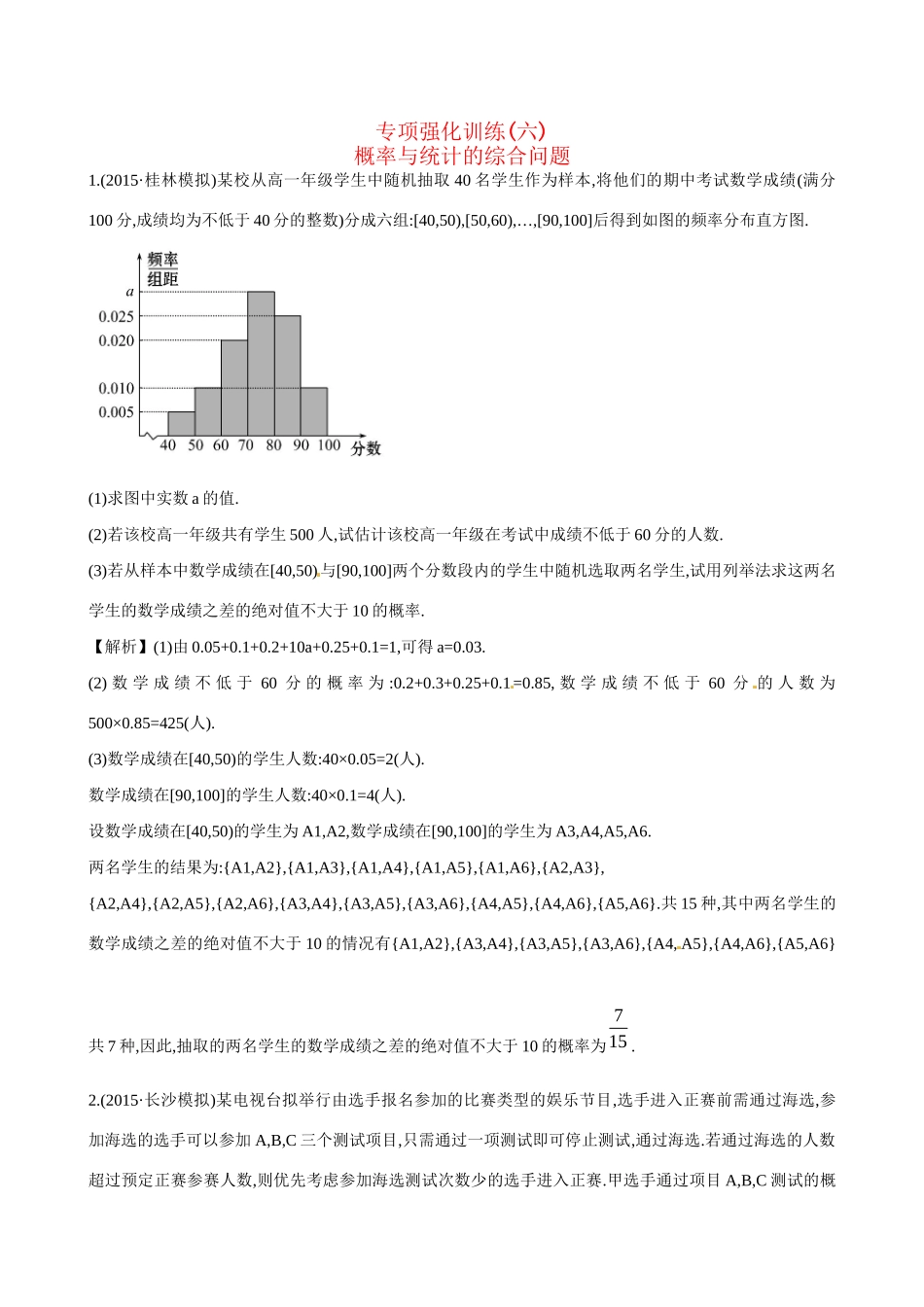
专项强化训练(六)概率与统计的综合问题1.(2015·桂林模拟)某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六组:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.(1)求图中实数a的值.(2)若该校高一年级共有学生500人,试估计该校高一年级在考试中成绩不低于60分的人数.(3)若从样本中数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,试用列举法求这两名学生的数学成绩之差的绝对值不大于10的概率.【解析】(1)由0.05+0.1+0.2+10a+0.25+0.1=1,可得a=0.03.(2)数学成绩不低于60分的概率为:0.2+0.3+0.25+0.1=0.85,数学成绩不低于60分的人数为500×0.85=425(人).(3)数学成绩在[40,50)的学生人数:40×0.05=2(人).数学成绩在[90,100]的学生人数:40×0.1=4(人).设数学成绩在[40,50)的学生为A1,A2,数学成绩在[90,100]的学生为A3,A4,A5,A6.两名学生的结果为:{A1,A2},{A1,A3},{A1,A4},{A1,A5},{A1,A6},{A2,A3},{A2,A4},{A2,A5},{A2,A6},{A3,A4},{A3,A5},{A3,A6},{A4,A5},{A4,A6},{A5,A6}.共15种,其中两名学生的数学成绩之差的绝对值不大于10的情况有{A1,A2},{A3,A4},{A3,A5},{A3,A6},{A4,A5},{A4,A6},{A5,A6}共7种,因此,抽取的两名学生的数学成绩之差的绝对值不大于10的概率为715.2.(2015·长沙模拟)某电视台拟举行由选手报名参加的比赛类型的娱乐节目,选手进入正赛前需通过海选,参加海选的选手可以参加A,B,C三个测试项目,只需通过一项测试即可停止测试,通过海选.若通过海选的人数超过预定正赛参赛人数,则优先考虑参加海选测试次数少的选手进入正赛.甲选手通过项目A,B,C测试的概率为分别为111,,532,且通过各次测试的事件相互独立.(1)若甲选手先测试A项目,再测试B项目,后测试C项目,求他通过海选的概率;若改变测试顺序,对他通过海选的概率是否有影响?说明理由.(2)若甲选手按某种顺序参加海选测试,第一项能通过的概率为p1,第二项能通过的概率为p2,第三项能通过的概率为p3,设他通过海选时参加测试的次数为ξ,求ξ的分布列和期望(用p1,p2,p3表示);并说明甲选手按怎样的测试顺序更有利于他进入正赛.【解析】(1)依题意,甲选手不能通过海选的概率为故甲选手能通过海选的概率为若改变测试顺序对他通过海选的概率没有影响,因为无论按什么顺序,其不能通过的概率均为即无论按什么顺序,其能通过海选的概率均为1115.(2)依题意,ξ的所有可能取值为1,2,3.P(ξ=1)=p1,P(ξ=2)=(1-p1)p2,P(ξ=3)=(1-p1)(1-p2)p3.故ξ的分布列为E(ξ)=p1+2(1-p1)p2+3(1-p1)(1-p2)p3,分别计算当甲选手按C→B→A,C→A→B,B→A→C,B→C→A,A→B→C,A→C→B的顺序参加测试时,E(ξ)的值,得甲选手按C→B→A的顺序参加测试时,E(ξ)最小,因为参加测试的次数少的选手优先进入正赛,故该选手选择将自己的优势项目放在前面,即按C→B→A的顺序参加测试更有利于进入正赛.3.(2015·重庆模拟)某单位实行休年假制度三年以来,50名职工休年假的次数进行的调查统计结果如表所示根据上表信息解答以下问题:(1)该单位任选两名职工,用η表示这两人休年假次数之和,“记函数f(x)=x2-ηx-1在区间(4,6)”上有且只有一个零点为事件A,求事件A发生的概率P(A).(2)从该单位任选两名职工,用ξ表示这两人休年假次数之差的绝对值,求随机变量ξ的分布列及数学期望E(ξ).【解析】(1)函数f(x)=x2-ηx-1过(0,-1)点,在区间(4,6)上有且只有一个零点,则必有f40,f60,即16410,1535:,36610,46解得所以,η=4或η=5.η=4与η=5为互斥事件,由互斥事件有一个发生的概率公式,所以P(A)=P1+P2=6812128.24549245(2)依题设可知ξ的可能取值为0,1,2,3.故ξ的分布列为:4.(2015·西安模拟)某煤矿发生透水事故时,作业区有若干人员被困.救援队从入口进入之后有L1,L2两条巷道通往作业区,L1巷道有A1,A2,A3三个易堵塞点,各点被堵塞的概率都是12;L2巷道有B1,B2两个易堵塞点,被堵塞的概率分别为33,45.(1)求L1巷道中,三个易堵塞点最多有一个被堵塞的概率.(2)若L2巷道中堵塞点个数为X,求X的分布列及数学期望E(X),“并按照平均堵塞点少的巷道是较好的抢...