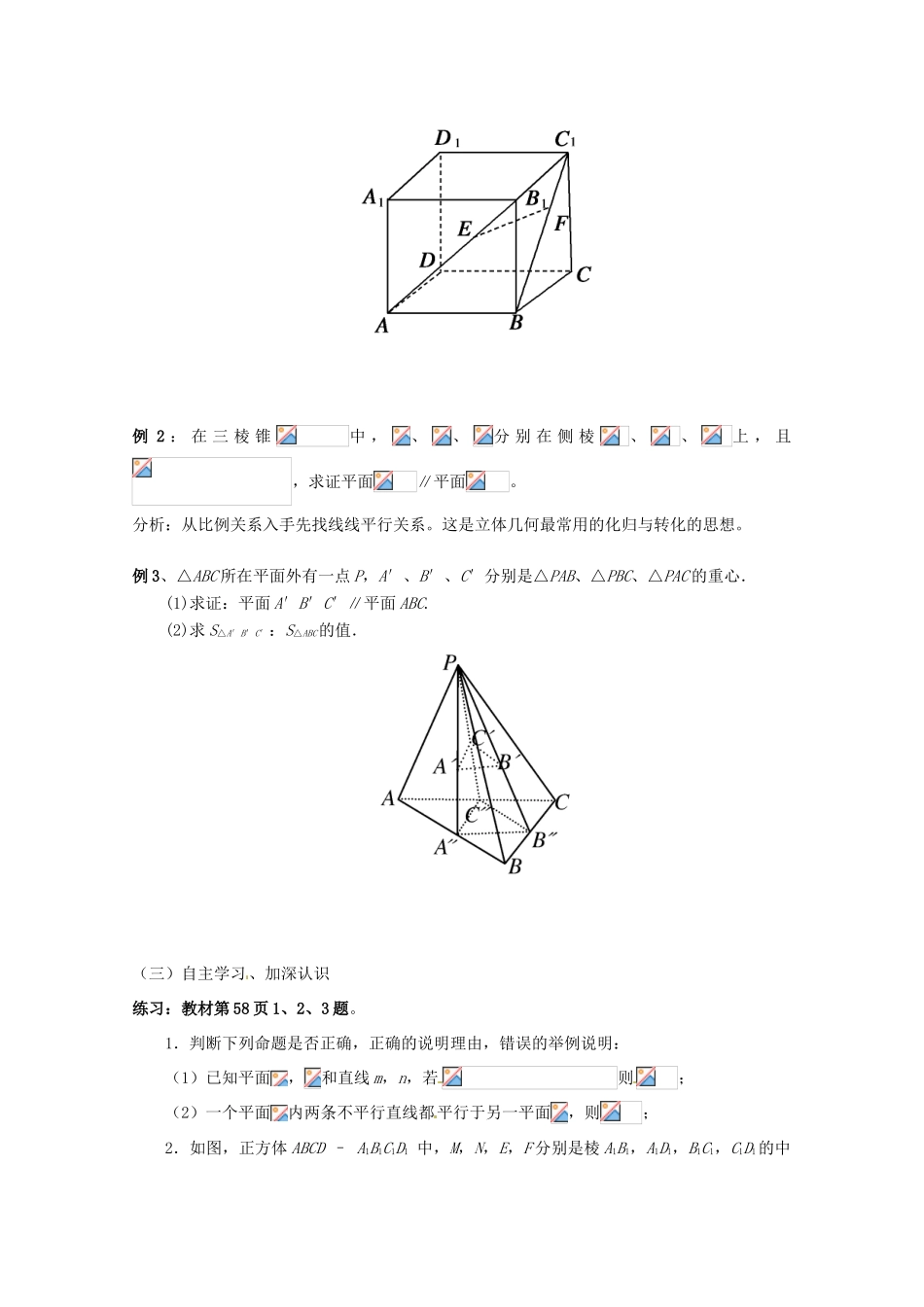
黑龙江省大庆外国语学校高一数学必修二第二章《2.2.2 平面与平面平行的判定》导学案教学重点、难点重点:两个平面平行的判定。难点:判定定理、例题的证明。教学过程直线与平面平行的判定定理_______________________________________。观察、思考教材第 56 页的观察题。(二)研探新知1、问题:(1)平面 β 内有一条直线与平面 α 平行,α、β 平行吗?(2)平面 β 内有两条直线与平面 α 平行,α、β 平行吗?两个平面平行的判定定理:一个平面内的两条交直线与另一个 平面平行,则这两个平面平行。符号表示:a βb βa∩b = P β∥αa∥αb∥α判断两平面平行的方法有三种:(1);(2);(3)2、解题示例例 1 如图所示,正方体 ABCD-A1B1C1D1中,E、F 分别在 B1A,C1B 上,且 EB1=AB1,C1F=C1B. 求证:(1)平面∥平面 (2)EF∥平面 ABCD.例 2 : 在 三 棱 锥中 ,、、分 别 在 侧 棱、、上 , 且,求证平面∥平面。分析:从比例关系入手先找线线平行关系。这是立体几何最常用的化归与转化的思想。例 3、△ABC 所在平面外有一点 P,A′、B′、C′分别是△PAB、△PBC、△PAC 的重心.(1)求证:平面 A′B′C′∥平面 ABC.(2)求 S△A′B′C′:S△ABC的值.(三)自主学习、加深认识练习:教材第 58 页 1、2、3 题。1.判断下列命题是否正确,正确的说明理由,错误的举例说明:(1)已知平面,和直线 m,n,若则;(2)一个平面内两条不平行直线都平行于另一平面,则;2.如图,正方体 ABCD – A1B1C1D1 中,M,N,E,F 分别是棱 A1B1,A1D1,B1C1,C1D1的中点. 求证:平面 AMN∥平面 EFDB.3.平面与平面平行的条件可以是( )A.内有无穷多条直线都与平行. B.直线 a∥,a∥,E 且直线 a 不在内,也不在内.C.直线,直线,且 a∥,b∥D.内的任何直线 都与平行.(四)归纳整理、整体认识1、判定定理中的线与线、线与面应具备什么条件?2、在本节课的学习过程中,还有哪些 不明白的地方,请向老师提出。(五)作业布置第 62 页习题 2.2 A 组第 7 题。