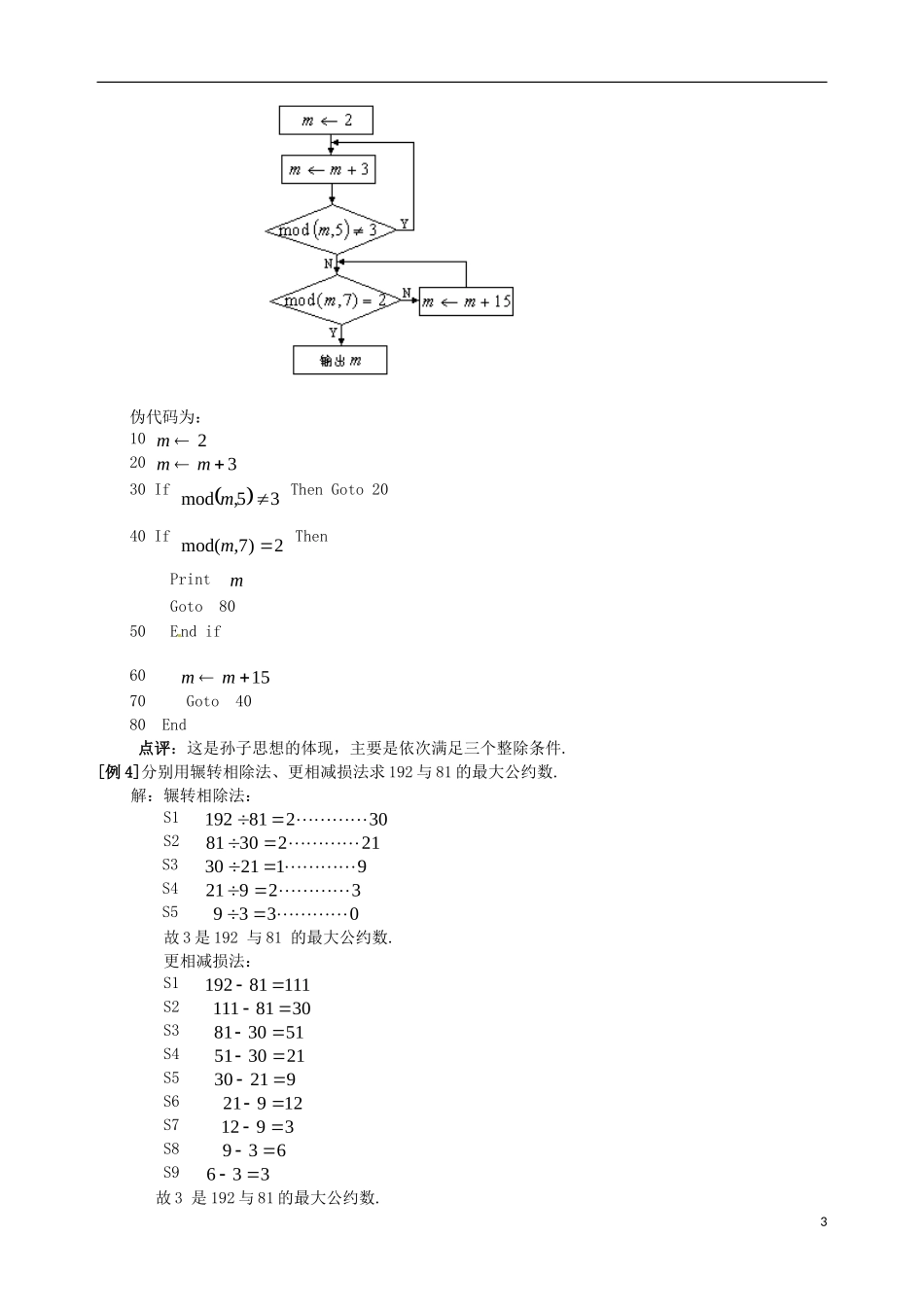
§ 13.3 算法案例一、知识导学1.算法设计思想:(1)“韩信点兵—孙子问题”对正整数 m 从 2 开始逐一检验条件,若三个条件中有任何一个不满足,则 m递增 1,一直到 m 同时满足三个条件为止(循环过程用 Goto 语句实现)(2)用辗转相除法找出ba. 的最大公约数的步骤是:计算出ba 的余数r ,若0r,则b 为ba,的最大公约数;若0r,则把前面的除数b 作为新的被除数,继续运算,直到余数为 0,此时的除数即为正整数ba,的最大公约数.2.更相减损术的步骤:(1)任意给出两个正数,判断它们是否都是偶数.若是,用 2 约简;若不是,执行第二步.(2)以较大的数减去较小的数,接着把较小的数与所得的差比较,并以大数减小数.继续这个操作,直到所得的数相等为止,则这个数(等数)就是所求的最大公约数.(3)二分法求方程0)(xf在区间ba,内的一个近似解 *x的解题步骤可表示为S1 取[ba,]的中点bax210,将区间 一分为二;S2 若 00 xf,则0x 就是方程的根;否则判别根x 在0x 的左侧还是右侧:若 00 xfaf,bxx,*0,以0x 代替a ;若 00 xfaf,则0,*xax ,以0x 代替b ;S3 若cba,计算终止,此时0xx ,否则转 S1.二、疑难知识导析 1.)int(x 表示不超过 x 的整数部分,如0)32.0int(,5)86.5int(,但当 x 是负数时极易出错,如1)14.1int(就是错误的,应为-2.2.),mod(ba表示a 除以b 所得的余数,也可用a mod b 表示.3.辗转相除法与更相减损术求最大公约数的联系与区别:(1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显.(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为 0 则得到,而更相减损术则以减数与差相等而得到.4.用二分法求方程近似解,必须先判断方程在给定区间 [ba,]上是否有解,即 xf连续且满足 0bfaf.并在二分搜索过程中需对中点处函数值的符号进行多次循环判定,故需要选择结构、循环结构,即可用 Goto 语句和条件语句实现算法.三、经典例题导讲[例 1])5int( , )05.0int( ,1 )9,67mod( , 45 mod 7= .A.16,-1,4,3 B.15,0,4,3 C.15,-1,3,4 D.15,-1,4,3错解:根据)int(x 表示不超过 x 的整...