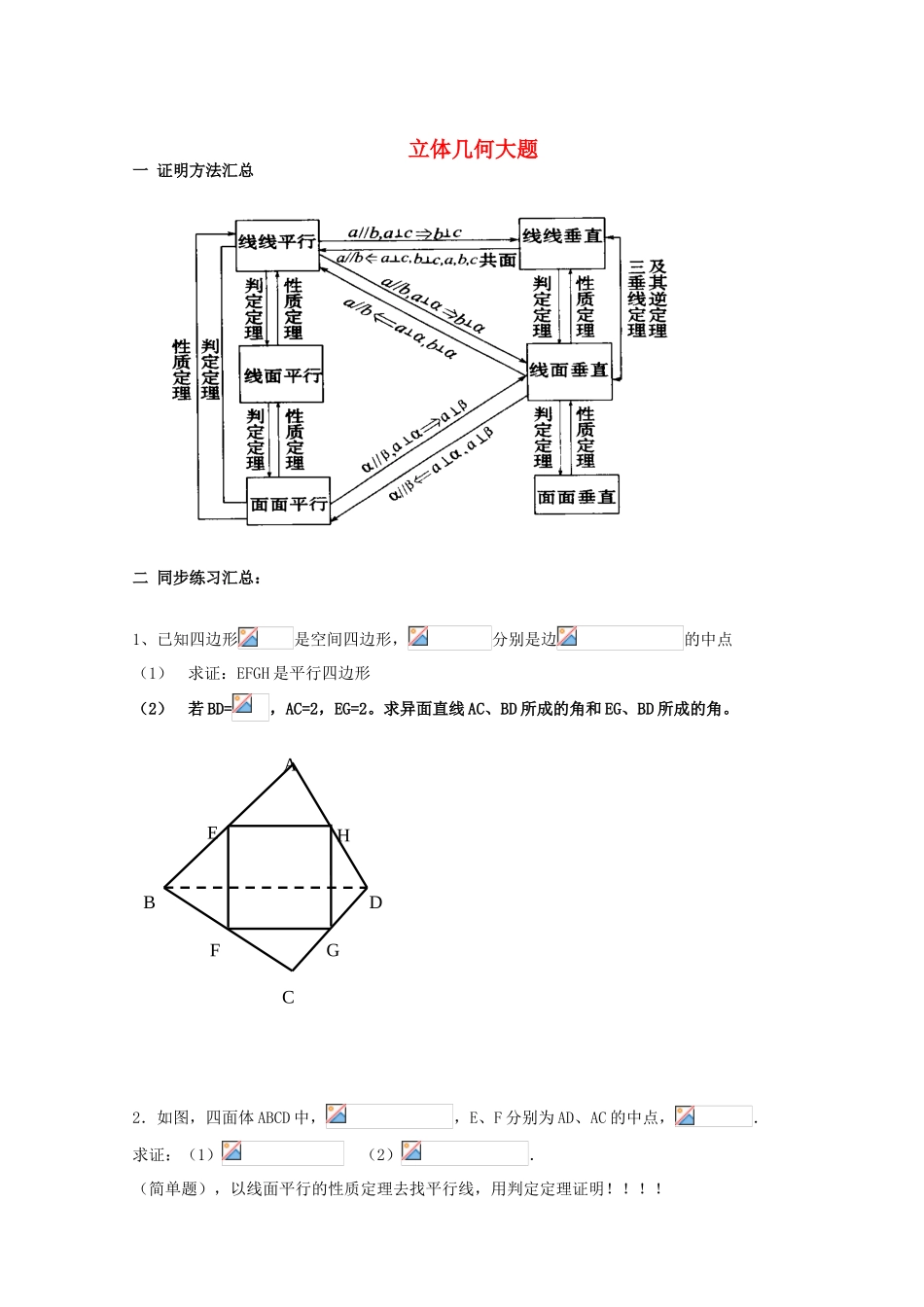
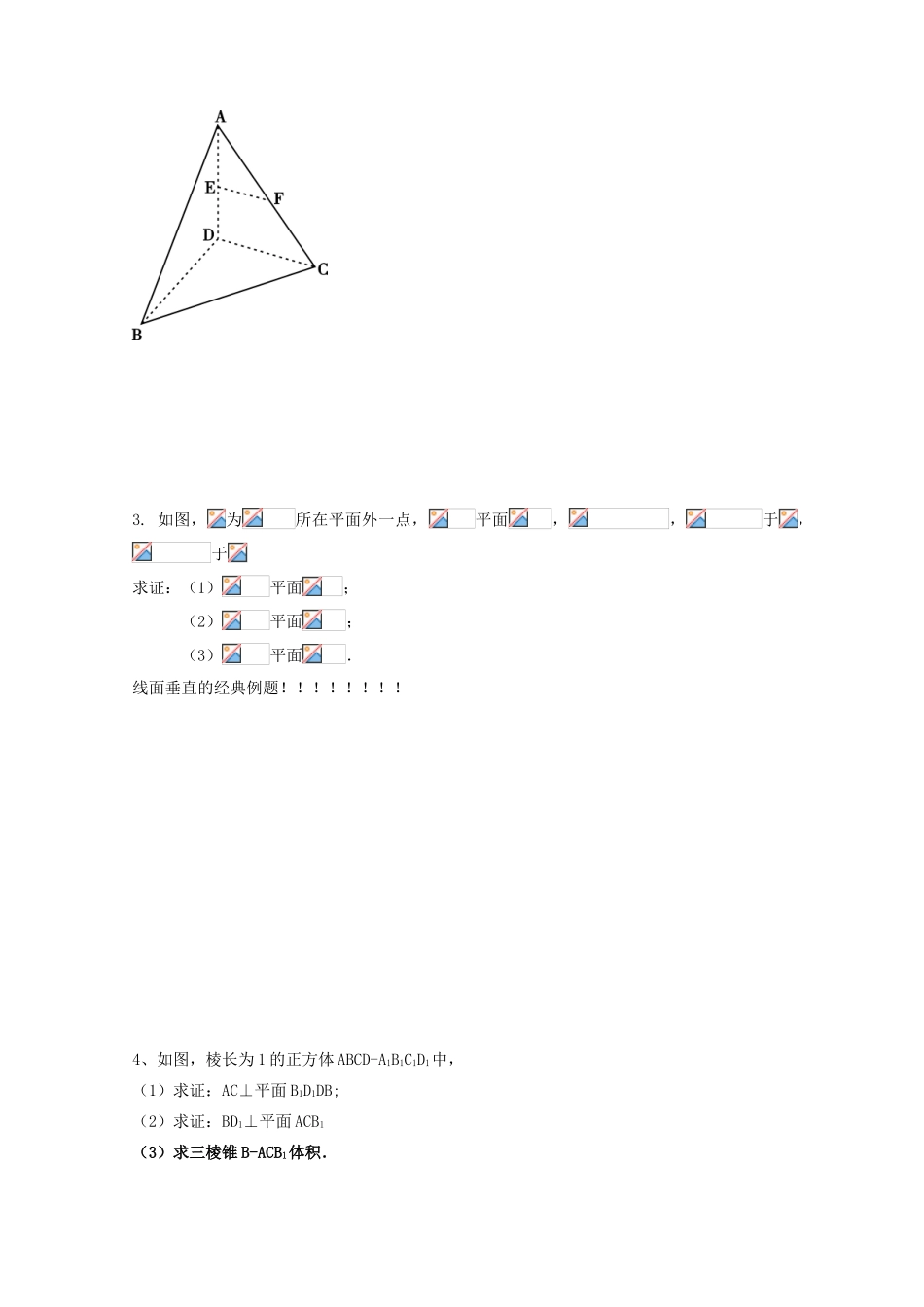
立体几何大题一 证明方法汇总二 同步练习汇总:1、已知四边形是空间四边形,分别是边的中点(1)求证:EFGH 是平行四边形(2)若 BD=,AC=2,EG=2。求异面直线 AC、BD 所成的角和 EG、BD 所成的角。 2.如图,四面体 ABCD 中,,E、F 分别为 AD、AC 的中点,.求证:(1) (2).(简单题),以线面平行的性质定理去找平行线,用判定定理证明!!!!AHGFEDCB3. 如图,为所在平面外一点,平面,,于,于求证:(1)平面;(2)平面;(3)平面.线面垂直的经典例题!!!!!!!!4、如图,棱长为 1 的正方体 ABCD-A1B1C1D1中,(1)求证:AC⊥平面 B1D1DB;(2)求证:BD1⊥平面 ACB1(3)求三棱锥 B-ACB1体积.5、已知正方体,是底对角线的交点.求证:(1) C1O∥面 (2 )面. 6、如图,ABCD 是正方形,O 是正方形的中心,PO底面 ABCD,E 是 PC 的中点求证:(1)PA∥平面 BDE(2)平面 PAC平面 BDE(3)若棱锥的棱长都为 2,求棱锥的体积。D1C1B1A1CDBA7.如图,PA⊥平面 ABC,平面 PAB⊥平面 PBC 求证:AB⊥BC 8.如图,在三棱锥 S-ABC 中,,(Ⅰ)证明 SC⊥BC;(Ⅱ)求侧面 SBC 与底面 ABC 所成二面角的大小。PABCBSCA9.在长方体中,已知,求异面直线与所成角的余弦值 。.(异面直线的夹角问题)10.如图,在三棱柱中,每个侧面均为正方形,为底边的中点,为侧棱的中点,与的交点为.(Ⅰ)求证:∥平面;(Ⅱ)求证:平面.DBCEB1C1AA1OB1A1C1BCAMNBCADEP11. 三 棱 柱中 , 侧 棱 与 底 面 垂 直 ,,, 分 别 是,的中点.(Ⅰ)求证://平面; (Ⅱ)求证:平面;(Ⅲ)求二面角的余弦值.计算引入垂直的证明(勾股定理)12. 如图:平面,四边形 ABCD 为直角梯形,//,,,,.(Ⅰ) 求证://平面;(Ⅱ) 求证:平面平面;(Ⅲ) 求二面角的余弦值.计算引入垂直的证明(勾股定理)13.如图,已知直三棱柱 ABC—A1B1C1,,E 是棱 CC1 上动点,F 是 AB 中点, (1)求证:; (2)当 E 是棱 CC1中点时,求证:CF//平面 AEB1; (3)在棱 CC1上是否存在点 E,使得二面角A—EB1—B 的大小是 45°,若存在,求 CE的长,若不存在,请说明理由。计算引入垂直的证明(勾股定理)14.在四棱锥中,侧面底面,,为中点,底面是直角梯形,,=90°,,.(I)求证:平面;(II)求证:平面;( III ) 设为 侧 棱上 一 点 ,, 试 确 定的 值 , 使...