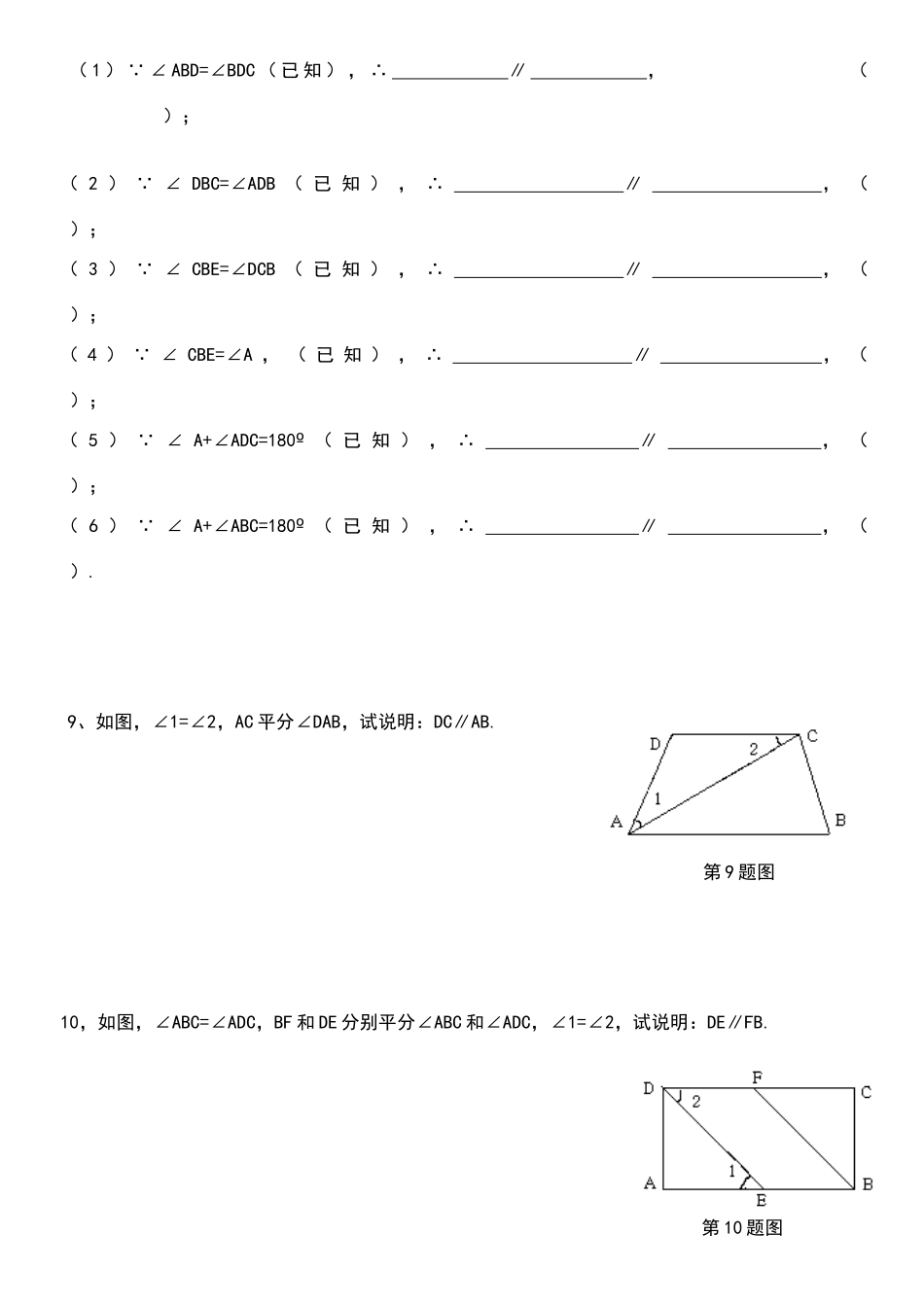
平行线与相交线 1,下列说法错误的是 ( )A、同位角不一定相等 B、 内错角都相等C、同旁内角可能相等 D、同旁内角互补则两直线平行2,在同一平面内,直线 与两条平行线 a,b 的位置关系是 ( )A. 一定与 a,b 都平行 B. 可能与 a 平行,与 b 相交C. 一定与 a,b 都相交 D. 与 a,b 都平行或都相交3,四边形 ABCD 中,若∠B+∠C=180º,则 AB 与 CD 的关系是( ) A.相交 B.平行 C.垂直 D.垂合4,同一平面内,下列说法:①过两点有且只有一条直线;②两直线不平行,则一定相交;③过一点有且只有一条直线与已知直线垂直;④过一点有且仅有一条直线与已知直线平行,其中正确的个数是 ( ) 个 个 个 个5,如图,下列条件能证明 AD∥BC 的是( ) A. ∠A=∠C B. ∠B=∠D C. ∠B=∠C D. ∠A+∠B=180º 第 5 题图 第 6 题图6,如图,直线 AB,CD 与 EF 相交于 G,H,下列条件:①∠1=∠2;②∠3=∠6;③∠2=∠8;④∠5∠8=180º,其中能判定 AB∥CD 的是( ) A. ①③ B. ①②④ C. ①③④ D. ②③④7、(1) ∠1=∠A(已知), ∴ ∥ ,( ); (2) ∠3=∠4(已知),∴ ∥ ,( )(第 7 题图);(3) ∠2=∠5(已知),∴ ∥ ,( );(4) ∠ADC+∠C=180º(已知),∴ ∥ ,( ).8,如图,( 1 ) ∠ ABD=∠BDC ( 已 知 ) , ∴ ∥ , ( );( 2 ) ∠ DBC=∠ADB ( 已 知 ) , ∴ ∥ , ( );( 3 ) ∠ CBE=∠DCB ( 已 知 ) , ∴ ∥ , ( );( 4 ) ∠ CBE=∠A , ( 已 知 ) , ∴ ∥ , ( );( 5 ) ∠ A+∠ADC=180º ( 已 知 ) , ∴ ∥ , ( );( 6 ) ∠ A+∠ABC=180º ( 已 知 ) , ∴ ∥ , ( ).9、如图,∠1=∠2,AC 平分∠DAB,试说明:DC∥AB. 第 9 题图 10,如图,∠ABC=∠ADC,BF 和 DE 分别平分∠ABC 和∠ADC,∠1=∠2,试说明:DE∥FB.第 10 题图11、作图题(用直尺和圆规作图,保留作图痕迹,要求写出作法)。 已知∠1,求作∠ACB,使∠ACB=∠1。 )12.如图 2-67,已知∠1=∠2,求∠3+∠4 的度数.答案:1,B 2,D 3,B 4,D 5,D 6,B 7,(1)AD∥BC,同位角相等,两直线平行;(2)AB∥CD,内错角相等,两直线平行; (3)AD∥BC,内错角相等,...