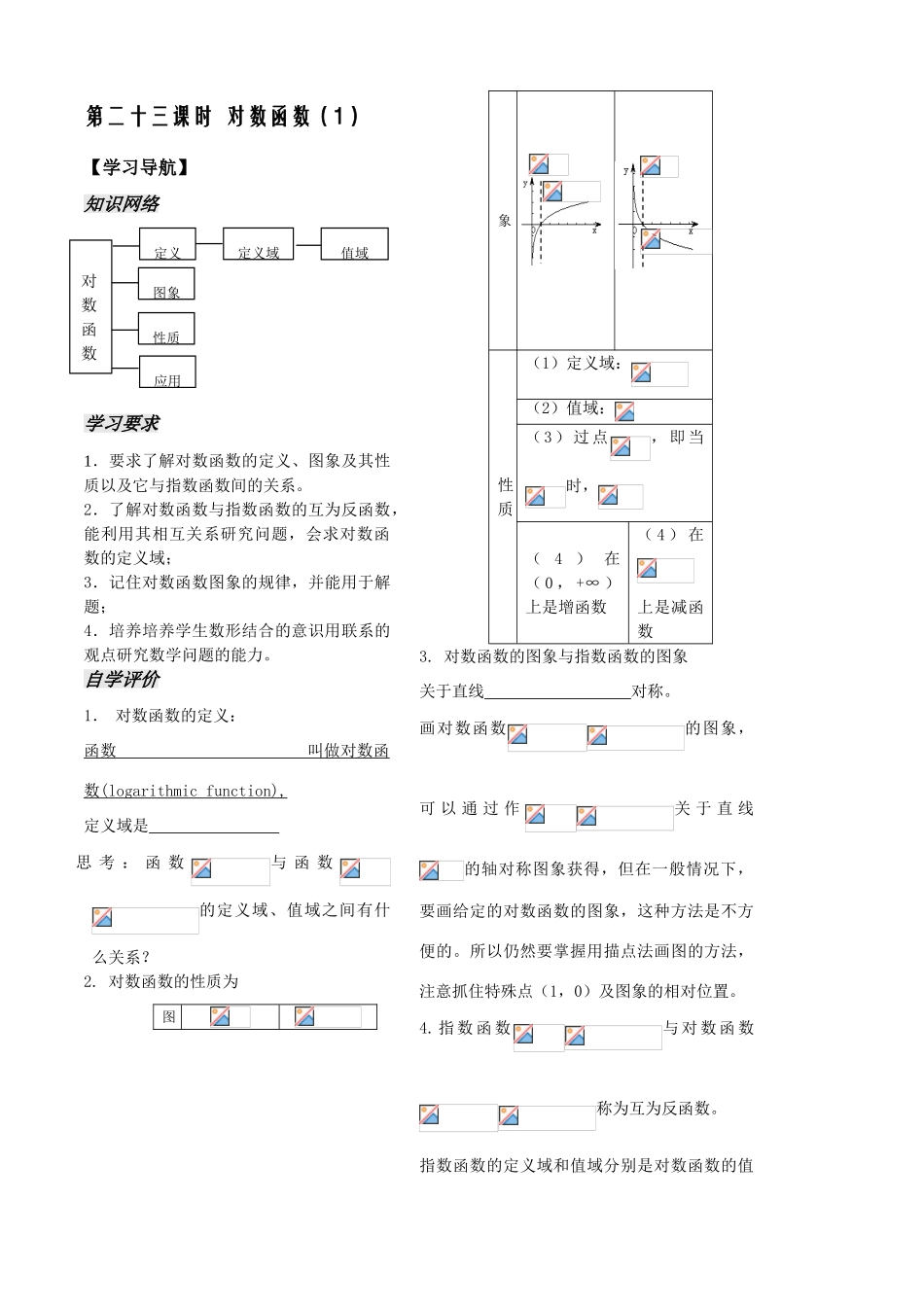
第二十三课时 对数函数(1)【学习导航】 知识网络 学习要求 1.要求了解对数函数的定义、图象及其性质以及它与指数函数间的关系。2.了解对数函数与指数函数的互为反函数,能利用其相互关系研究问题,会求对数函数的定义域;3.记住对数函数图象的规律,并能用于解题;4.培养培养学生数形结合的意识用联系的观点研究数学问题的能力。自学评价1. 对数函数的定义:函数 叫做对数函数 (logarithmic function), 定义域是 思 考 : 函 数与 函 数的定义域、值域之间有什么关系?2. 对数函数的性质为图象性质(1)定义域:(2)值域:(3)过点,即当时,( 4 ) 在( 0 , +∞ )上是增函数( 4 ) 在上是减函数3. 对数函数的图象与指数函数的图象关于直线 对称。画对数函数的图象,可 以 通 过 作关 于 直 线的轴对称图象获得,但在一般情况下,要画给定的对数函数的图象,这种方法是不方便的。所以仍然要掌握用描点法画图的方法,注意抓住特殊点(1,0)及图象的相对位置。4. 指 数 函 数与 对 数 函 数称为互为反函数。指数函数的定义域和值域分别是对数函数的值数图象性质值域定义域定义应用对函数域和定义域。5.一般地,如果函数存在反函数,那么它的反函数,记作 思考:互为反函数的两个函数的定义域和值域有什么关系?原函数的定义域和值域分别是反函数的值域和定义域。【精典范例】例 1:求下列函数的定义域(1); (2) ; (3) (4)[ 分 析 ] : 此 题 主 要 利 用 对 数 函 数的定义域求解。例 2:利用对数函数的性质,比较下列各组数中两个数的大小:(1),; (2),;(3),; (4),,点评: 本例是利用对数函数的增减性比较两个对数的大小,当不能直接进行比较时,可在两个对数中间插入一个已知数(如 1 或 0),间接比较上述两个对数的大小。例 3 若且,求的取值范围 (2)已知,求的取值范围;点评:本题的关键是利用对数函数的单调性解不等式,一定要注意对数函数定义域。追踪训练一1.求函数的定义域,并画出函数的图象。2. 比较下列各组数中两个值的大小:(1),; (2),;(3),.(4),,3.解下列方程:(1) (2)(3)(4)4.解不等式:(1)(2) 学生质疑教师释疑