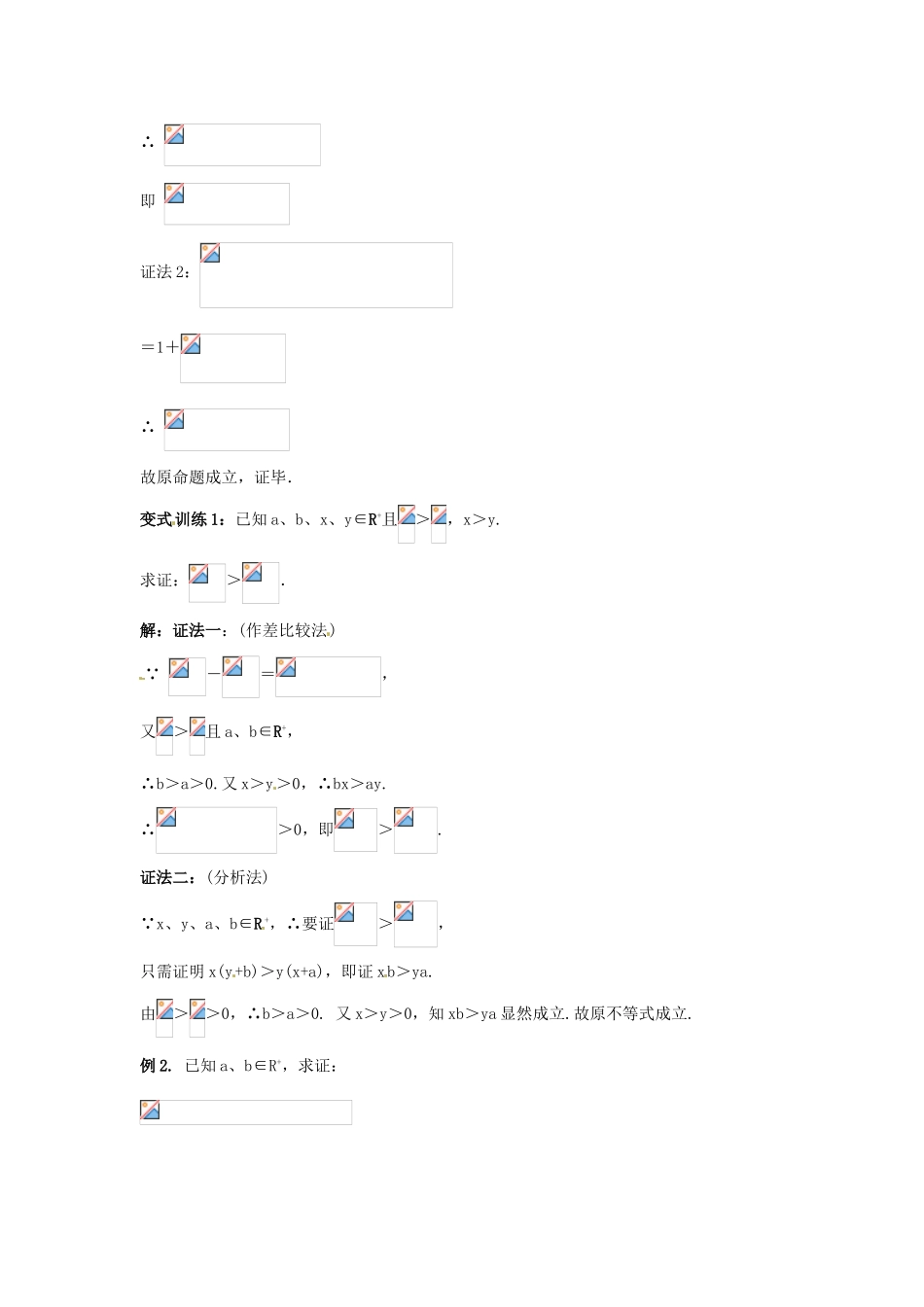
]福建省长泰一中高考数学一轮复习《不等式证明》(一)学案 1.比较法是证明不等式的一个最基本的方法,分比差、比商两种形式.(1)作差比较法,它的依据是: 它的基本步骤:作差——变形——判断,差的变形的主要方法有配方法,分解因式法,分子有理化等.(2) 作商比较法,它的依据是:若>0, >0,则例 1. 已知,求证:证法 1:===∵>0,>0,典型例题基础过关∴ 即 证法 2:=1+∴ 故原命题成立,证毕.变式训练 1:已知 a、b、x、y∈R+且>,x>y.求证:>.解:证法一:(作差比较法)∵ -=,又>且 a、b∈R+,∴b>a>0.又 x>y>0,∴bx>ay.∴>0,即>.证法二:(分析法)∵x、y、a、b∈R +,∴要证>,只需证明 x(y+b)>y(x+a),即证 xb>ya.由>>0,∴b>a>0. 又 x>y>0,知 xb>ya 显然成立.故原不等式成立.例 2. 已知 a、b∈R+,求证:∴ 变式训练 3:若为△ABC 的三条边,且,则( )A. B. C. D.答案:D.解析:,又∵∴。例 4. 设二次函数,方程的两个根、满足.(1) 当 x∈(0,x1)时,证明:x