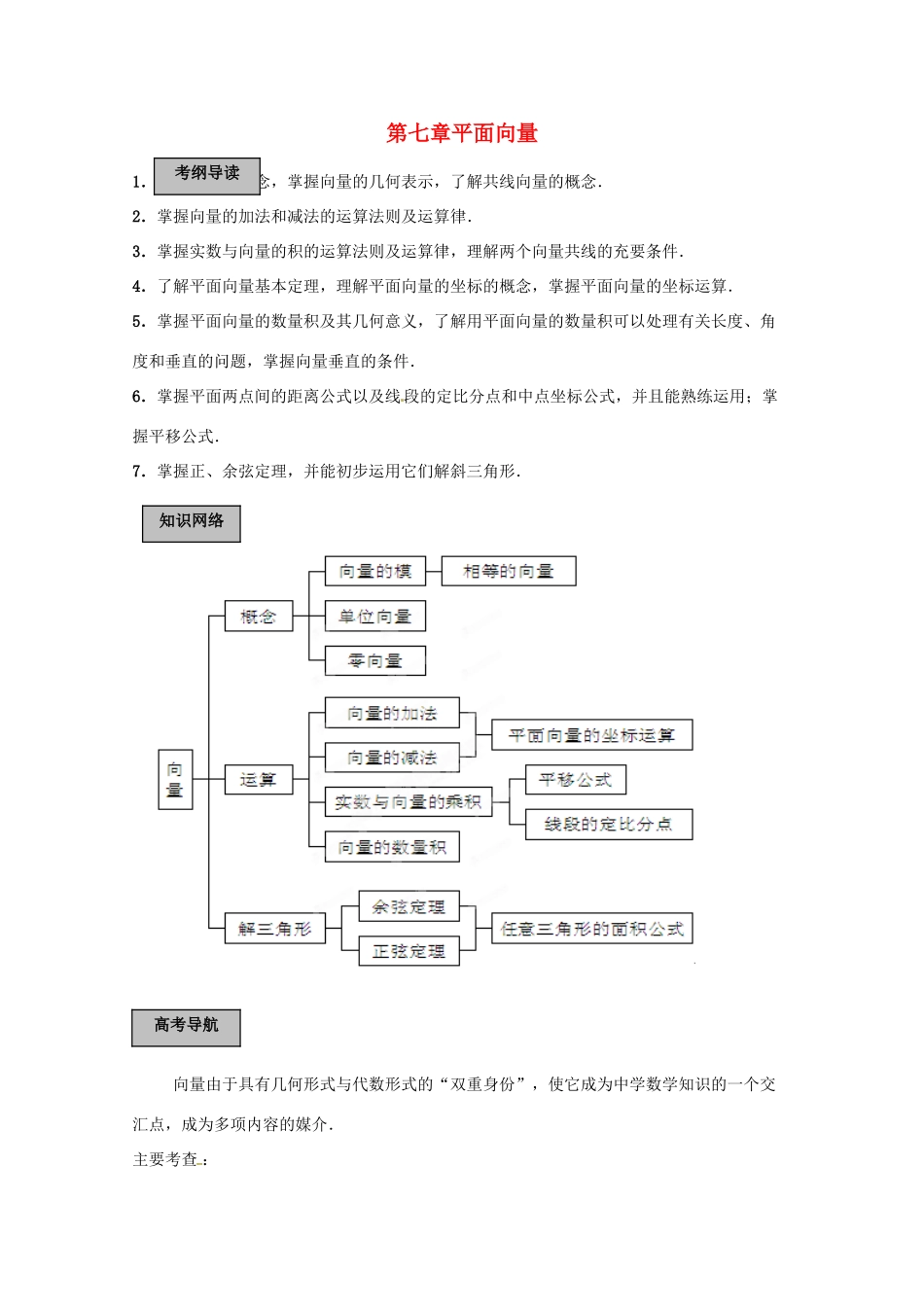
第七章平面向量1.理解向量的概念,掌握向量的几何表示,了解共线向量的概念.2.掌握向量的加法和减法的运算法则及运算律.3.掌握实数与向量的积的运算法则及运算律,理解两个向量共线的充要条件.4.了解平面向量基本定理,理解平面向量的坐标的概念,掌握平面向量的坐标运算.5.掌握平面向量的数量积及其几何意义,了解用平面向量的数量积可以处理有关长度、角度和垂直的问题,掌握向量垂直的条件.6.掌握平面两点间的距离公式以及线段的定比分点和中点坐标公式,并且能熟练运用;掌握平移公式.7.掌握正、余弦定理,并能初步运用它们解斜三角形.向量由于具有几何形式与代数形式的“双重身份”,使它成为中学数学知识的一个交汇点,成为多项内容的媒介.主要考查 :知识网络考纲导读高考导航1.平面向量的性质和运算法则,共线定理、基本定理、平行四边形法则及三角形法则.2.向量的坐标运算及应用.3.向量和其它数学知识的结合.如和三角函数、数列、曲线方程等及向量在物理中的应用.4.正弦定理、余弦定理及利用三角公式进行恒等变形的能力.以化简、求值或判断三角形的形状为主.解三角形常常作为解题工具用于立体几何中的计算或证明.第 1 课时 向量的概念与几何运算⑵ (μ)= . (+μ)= . (+ )= .⑶ 共线定理:向量 与非零向量共线的充要条件是有且只有一个实数 λ 使得 .4.⑴ 平面向量基本定理:如果、是同一平面内的两个不共线的向量,那么对于这一平面内的任一向量,有且只有一对实数、,使得 .⑵ 设、是一组基底,=, =,则与 共线的充要条件是 .例 1.已知△ABC 中,D 为 BC 的中点,E 为 AD 的中点.设,,求.典型例题基础过关解:=-=(+)-=-+变式训练 1.如图所示,D 是△ABC 边 AB 上的中点,则向量等于( )A.-+B.--C.-D.+解:A例 2. 已知向量,,,其中、不共线,求实数、,使.解: =λ+μ2-9=(2λ+2μ)+(-3λ+3μ)2λ+2μ=2,且-3λ+3μ=-9λ=2,且 μ=-1变式训练 2:已知平行四边形 ABCD 的对角线相交于 O 点,点 P 为平面上任意一点,求证:证明 +=2,+=2+++=4例 3. 已知 ABCD 是一个梯形,AB、CD 是梯形的两底边,且 AB=2CD,M、N 分别是 DC 和 AB 的中点,若,,试用、表示和.解:连 NC,则;变式训练 3:如图所示,OADB 是以向量=,= 为邻边的平行四边形,又=,=,试用、 表示,,...