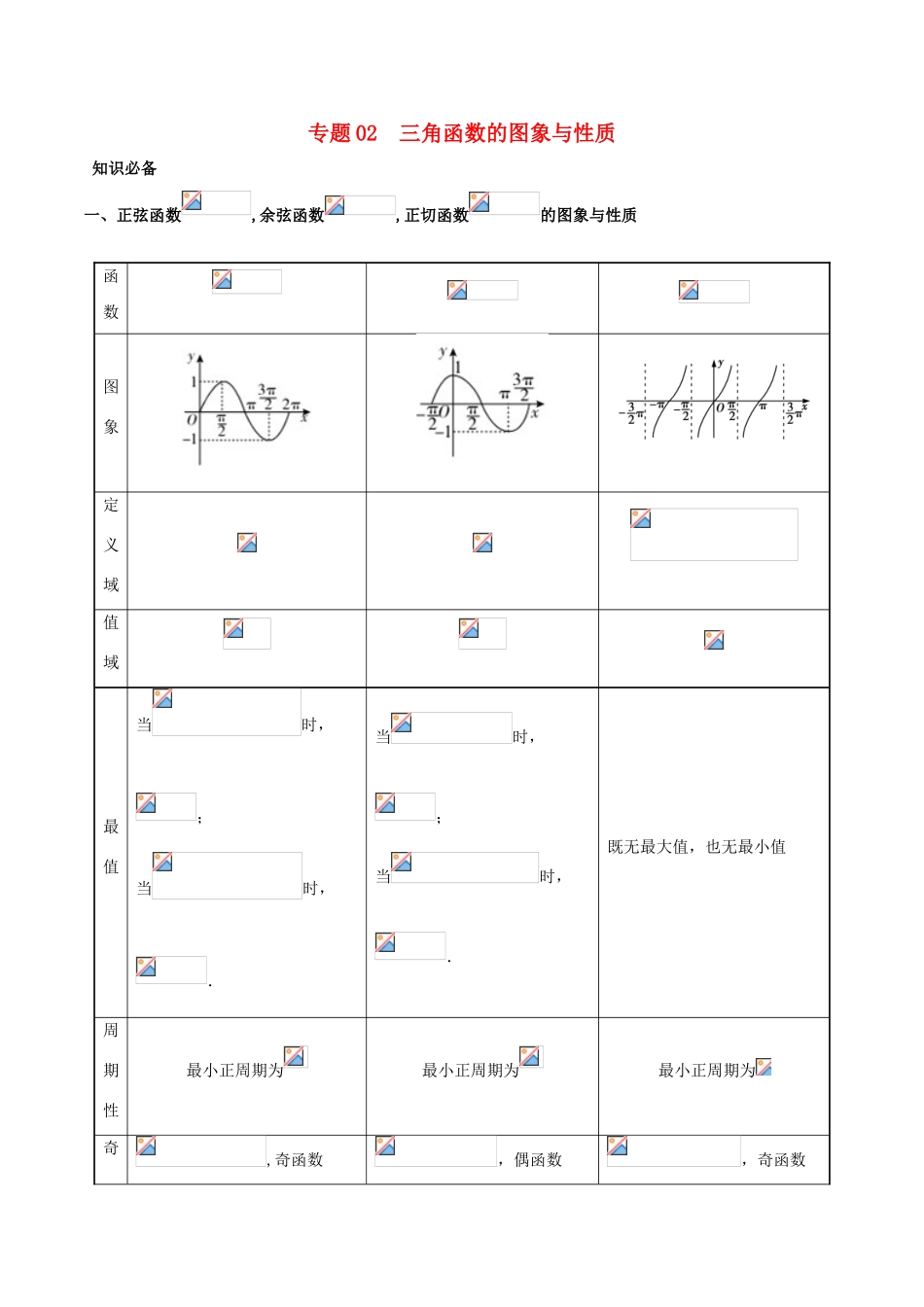
专题 02 三角函数的图象与性质知识必备一、正弦函数,余弦函数,正切函数的图象与性质函数图象定义域值域最值当时,;当时,.当时,;当时,.既无最大值,也无最小值周期性最小正周期为最小正周期为最小正周期为奇,奇函数,偶函数,奇函数偶性单调性在上是增函数;在上是减函数.在上是增函数;在上是减函数.在上是增函数.对称性对称中心;对称轴,既是中心对称图形又是轴对称图形.对称中心;对称轴,既是中心对称图形又是轴对称图形.对称中心;无对称轴,是中心对称图形但不是轴对称图形.二、函数的图象与性质1.函数的图象的画法(1)变换作图法由函数的图象通过变换得到(A>0,ω>0)的图象,有两种主要途径:“先平移后伸缩”与“先伸缩后平移”.如下图. (2)五点作图法找五个关键点,分别为使 y 取得最小值、最大值的点和曲线与 x 轴的交点.其步骤为: ① 先确定最小正周期 T=,在一个周期内作出图象; ② 令,令 X 分别取 0,,,,求出对应的 x 值,列表如下:由此可得五个关键点; ③ 描点画图,再利用函数的周期性把所得简图向左右分别扩展,从而得到的简图.2.函数(A>0,ω>0)的性质(1)奇偶性:时,函数为奇函数;时,函数为偶函数. (2)周期性:存在周期性,其最小正周期为 T= .(3)单调性:根据 y=sint 和 t=的单调性来研究,由得单调增区间;由得单调减区间. (4)对称性:利用 y=sin x 的对称中心为求解,令,求得 x. 利用 y=sin x 的对称轴为求解,令,得其对称轴.3.函数(A>0,ω>0)的物理意义当函数(A>0,ω>0,)表示一个简谐振动量时,则 A 叫做振幅,T=叫做周期,f =叫做频率,叫做相位,x=0 时的相位叫做初相.核心考点考点一 三角函数的图象与性质【例 1】(奇偶性与对称性)已知函数在处取得最大值,则函数是A.偶函数且它的图象关于点对称 B.偶函数且它的图象关于点对称C.奇函数且它的图象关于点对称 D.奇函数且它的图象关于点对称【答案】B 备考指南1.对于函数 y=Asin(ωx+φ),其对称轴一定经过图象的最高点或最低点,对称中心的横坐标一定是函数的零点,因此在判断直线 x=x0或点(x0,0)是否为函数的对称轴或对称中心时,可通过检验f(x0)的值进行判断.2.若 f(x)=Asin(ωx+φ)为偶函数,则 φ=kπ+(kZ),同时当 x=0 时,f(x)取得最大或最小值.若 f(x)=Asin(ωx+φ)为奇函数,则 φ=kπ(k∈Z),同时当 x=0 时,f(x)=0.【例 2】(...