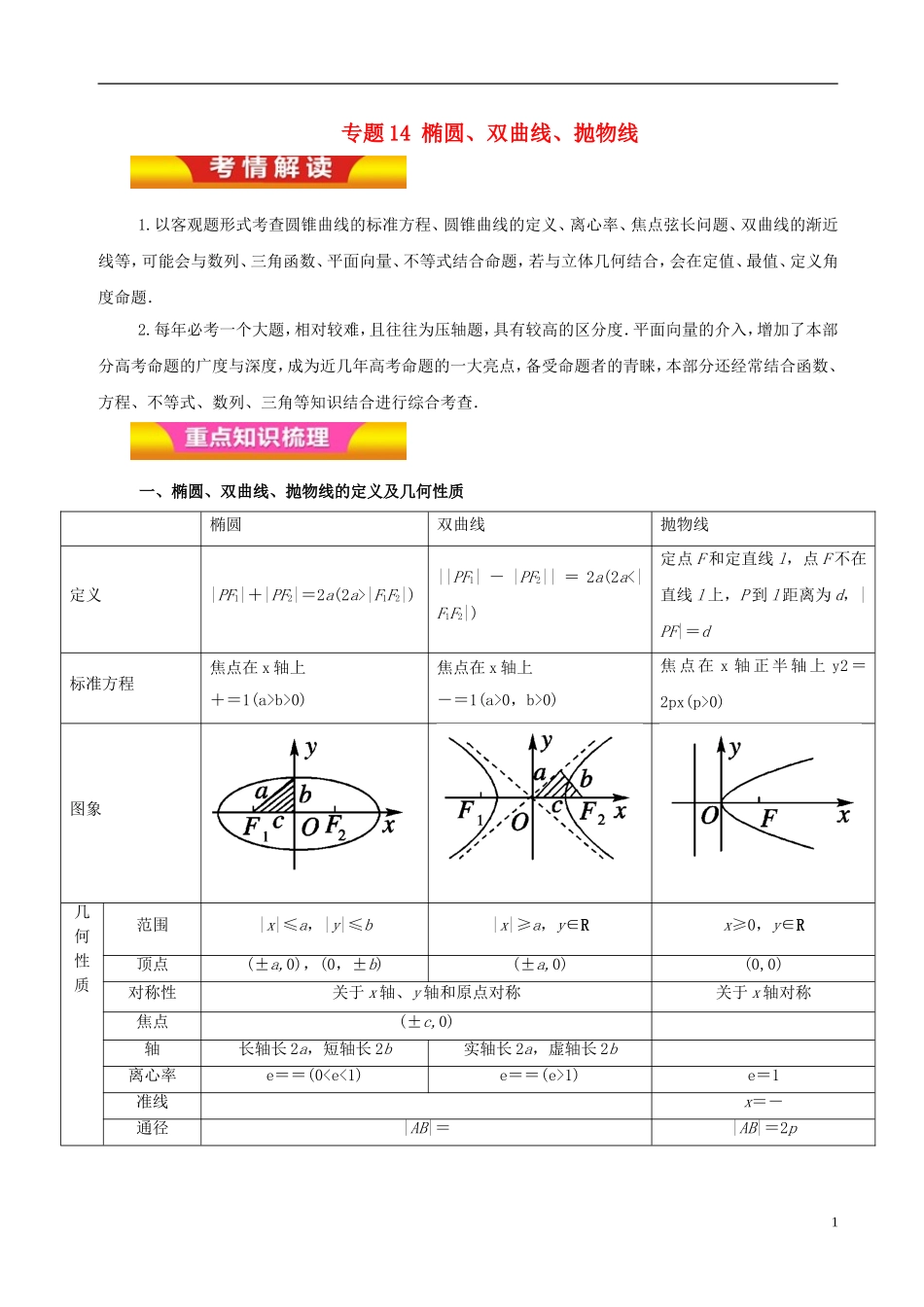
专题 14 椭圆、双曲线、抛物线1.以客观题形式考查圆锥曲线的标准方程、圆锥曲线的定义、离心率、焦点弦长问题、双曲线的渐近线等,可能会与数列、三角函数、平面向量、不等式结合命题,若与立体几何结合,会在定值、最值、定义角度命题.2.每年必考一个大题,相对较难,且往往为压轴题,具有较高的区分度.平面向量的介入,增加了本部分高考命题的广度与深度,成为近几年高考命题的一大亮点,备受命题者的青睐,本部分还经常结合函数、方程、不等式、数列、三角等知识结合进行综合考查.一、椭圆、双曲线、抛物线的定义及几何性质椭圆双曲线抛物线定义|PF1|+|PF2|=2a(2a>|F1F2|)||PF1| - |PF2|| = 2a(2a<|F1F2|)定点 F 和定直线 l,点 F 不在直线 l 上,P 到 l 距离为 d,|PF|=d标准方程焦点在 x 轴上+=1(a>b>0)焦点在 x 轴上-=1(a>0,b>0)焦 点 在 x 轴 正 半 轴 上 y2 =2px(p>0)图象几何性质范围|x|≤a,|y|≤b|x|≥a,y∈Rx≥0,y∈R顶点(±a,0),(0,±b)(±a,0)(0,0)对称性关于 x 轴、y 轴和原点对称关于 x 轴对称焦点(±c,0)轴长轴长 2a,短轴长 2b实轴长 2a,虚轴长 2b离心率e==(01)e=1准线x=-通径|AB|=|AB|=2p1渐近线y=±x【误区警示】1.求椭圆、双曲线方程时,注意椭圆中 c2=a2+b2,双曲线中 c2=a2-b2的区别.2.注意焦点在 x 轴上与 y 轴上的双曲线的渐近线方程的区别.3.平行于双曲线渐近线的直线与双曲线有且仅有一个交点;平行于抛物线的轴的直线与抛物线有且仅有一个交点.考点一 椭圆的定义及其方程例 1.【2017 课标 3,文 11】已知椭圆 C:22221xyab ,(a>b>0)的左、右顶点分别为 A1,A2,且以线段A1A2为直径的圆与直线20bxayab 相切,则 C 的离心率为( )A. 63 B. 33 C.23D. 13【答案】A【变式探究】【2016 高考浙江文数】已知椭圆 C1:22xm+y2=1(m>1)与双曲线 C2:22xn–y2=1(n>0)的焦点重合,e1,e2分别为 C1,C2的离心率,则( )A.m>n 且 e1e2>1 B.m>n 且 e1e2<1 C.m1 D.mb>0)的右焦点为...