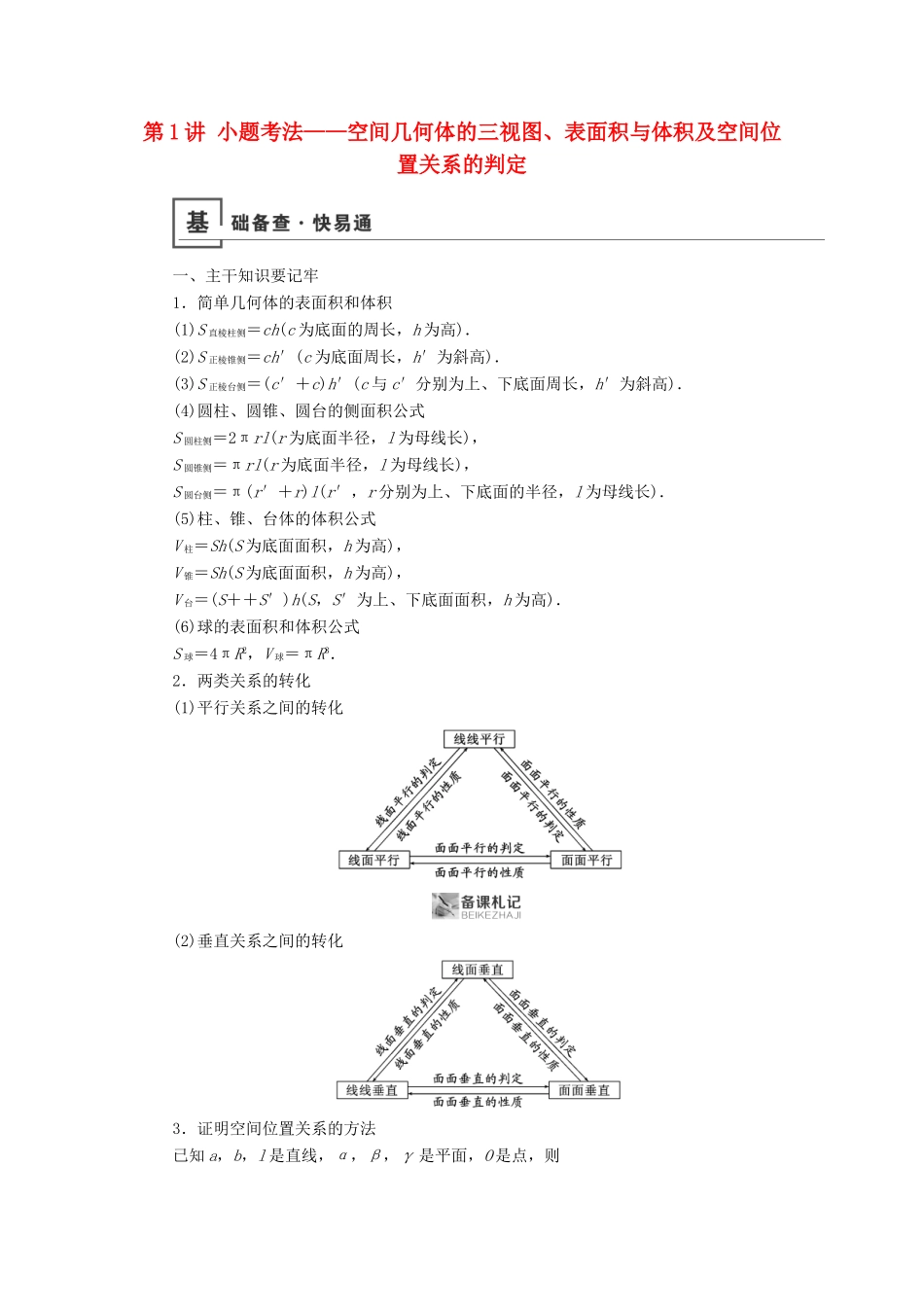
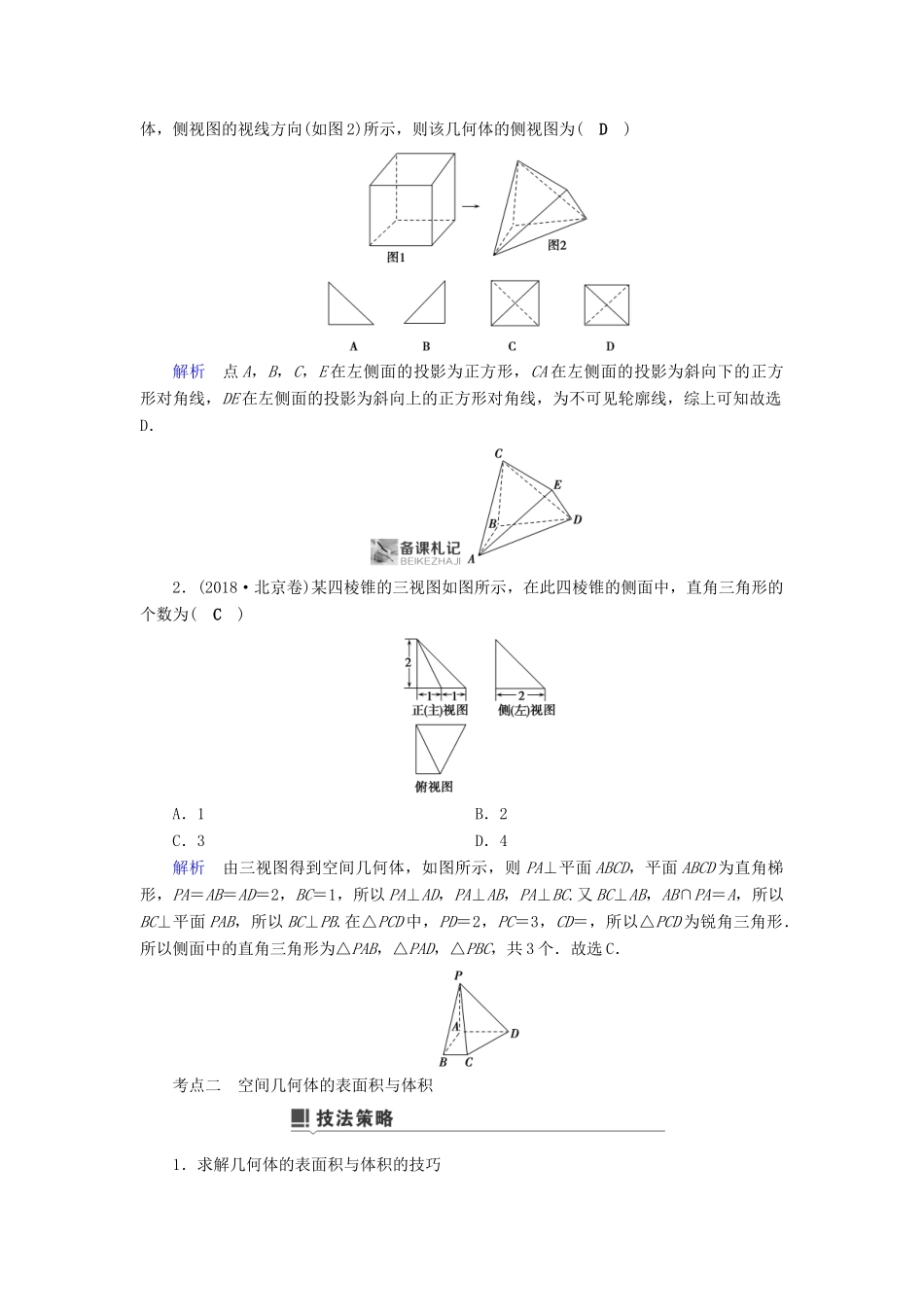
第 1 讲 小题考法——空间几何体的三视图、表面积与体积及空间位置关系的判定一、主干知识要记牢1.简单几何体的表面积和体积(1)S 直棱柱侧=ch(c 为底面的周长,h 为高).(2)S 正棱锥侧=ch′(c 为底面周长,h′为斜高).(3)S 正棱台侧=(c′+c)h′(c 与 c′分别为上、下底面周长,h′为斜高).(4)圆柱、圆锥、圆台的侧面积公式S 圆柱侧=2πrl(r 为底面半径,l 为母线长),S 圆锥侧=πrl(r 为底面半径,l 为母线长),S 圆台侧=π(r′+r)l(r′,r 分别为上、下底面的半径,l 为母线长).(5)柱、锥、台体的体积公式V 柱=Sh(S 为底面面积,h 为高),V 锥=Sh(S 为底面面积,h 为高),V 台=(S++S′)h(S,S′为上、下底面面积,h 为高).(6)球的表面积和体积公式S 球=4πR2,V 球=πR3.2.两类关系的转化(1)平行关系之间的转化(2)垂直关系之间的转化3.证明空间位置关系的方法已知 a,b,l 是直线,α,β,γ 是平面,O 是点,则(1)线线平行:⇒c∥b,⇒a∥b,⇒a∥b, ⇒a∥b.(2)线面平行:⇒a∥α,⇒a∥α, ⇒a∥α.(3)面面平行:⇒α∥β, ⇒α∥β, ⇒α∥γ.(4)线线垂直:⇒a⊥b, ⇒a⊥b.(5)线面垂直: ⇒l⊥α, ⇒a⊥β,⇒a⊥β ⇒b⊥α.(6)面面垂直:⇒α⊥β, ⇒α⊥β.二、二级结论要用好1.长方体的对角线与其共点的三条棱之间的长度关系 d2=a2+b2+c2;若长方体外接球半径为 R,则有(2R)2=a2+b2+c2.2.棱长为 a 的正四面体的内切球半径 r=a,外接球的半径 R=a.又正四面体的高 h=a,故 r=h,R=h.三、易错易混要明了应用空间线面平行与垂直关系中的判定定理和性质定理时,忽视判定定理和性质定理中的条件,导致判断出错.如由 α⊥β,α∩β=l,m⊥l,易误得出 m⊥β 的结论,就是因为忽视面面垂直的性质定理中 m⊂α 的限制条件.考点一 空间几何体的三视图1.由直观图确定三视图的方法根据空间几何体三视图的定义及画法规则和摆放规则确定.2.由三视图还原到直观图的思路(1)根据俯视图确定几何体的底面.(2)根据正(主)视图或侧(左)视图确定几何体的侧棱与侧面的特征,调整实线和虚线所对应的棱、面的位置.(3)确定几何体的直观图形状.1.(2018·湖北联考)将正方体(如图 1)截去三个三棱锥后,得到(如图 2)所示的几何体,侧视图的视线方向(如图 2)所示,则该几何体的侧视图为( D )解析 点 A,B,C,E 在左侧面的投影为正方形,CA...