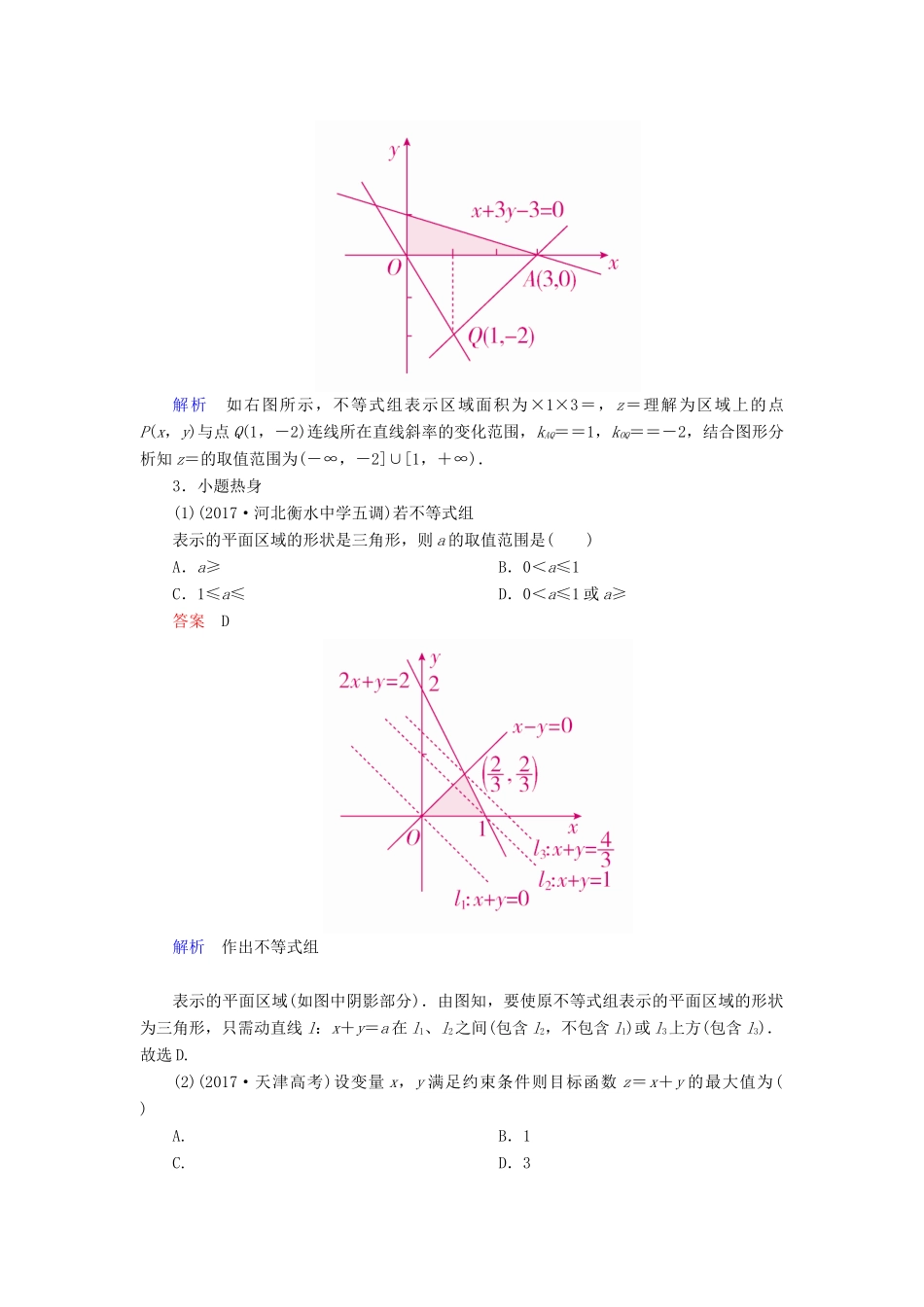
6.2 二元一次不等式(组)与简单的线性规划问题[知识梳理]1.二元一次不等式(组)表示的平面区域不等式表示区域Ax+By+C >0直线 Ax+By+C=0 某一侧的所有点组成的平面区域不包括边界直线Ax+By+C ≥0包括边界直线不等式组各个不等式所表示平面区域的公共部分2.线性规划相关概念名称意义约束条件由变量 x,y 组成的一次不等式线性约束条件由 x,y 的一次不等式(或方程)组成的不等式组目标函数欲求最大值或最小值的函数线性目标函数关于 x,y 的一次解析式可行解满足线性约束条件的解可行域所有可行解组成的集合最优解使目标函数取得最大值或最小值的可行解线性规划问题在线性约束条件下求线性目标函数的最大值或最小值问题3.重要结论(1)直线定界:不等式中无等号时直线画成虚线,有等号时直线画成实线;特殊点定域:若直线不过原点,特殊点常选原点;若直线过原点,则特殊点常选取(0,1)或(1,0)来验证.(2)利用“同号上,异号下”判断二元一次不等式表示的平面区域:对于 Ax+By+C>0 或 Ax+By+C<0,则有① 当 B(Ax+By+C)>0 时,区域为直线 Ax+By+C=0 的上方;② 当 B(Ax+By+C)<0 时,区域为直线 Ax+By+C=0 的下方.(3)最优解和可行解的关系最优解必定是可行解,但可行解不一定是最优解.最优解有时唯一,有时有多个.4.利用线性规划求最值,用图解法求解的步骤(1)作可行域;(2)将目标函数进行变形;(3)确定最优解;(4)求最值.[诊断自测]1.概念思辨(1)不等式 Ax+By+C>0 表示的平面区域一定在直线 Ax+By+C=0 的上方.( )(2)不等式 x2-y2<0 表示的平面区域是一、三象限角平分线和二、四象限角平分线围成的含有 y 轴的两块区域.( )(3)线性目标函数的最优解可能是不唯一的.( )(4)目标函数 z=ax+by(b≠0)中,z 的几何意义是直线 ax+by-z=0 在 y 轴上的截距.( )答案 (1)× (2)√ (3)√ (4)×2.教材衍化(1)(必修 A5P86T3)不等式组表示的平面区域是( )答案 B解析 x-3y+6≥0 表示直线 x-3y+6=0 及其下方部分,x-y+2<0 表示直线 x-y+2=0 上方部分,故不等式表示的平面区域为选项 B.故选 B.(2)(必修 A5P93B 组 T1)若实数 x,y 满足则不等式组表示区域的面积为________,z=的取值范围是________.答案 (-∞,-2]∪[1,+∞)解析 如右图所示,不等式组表示区域面积为×1×3=,z=理解为区域上的点P(x,y)与点 Q(1,-2)连线所在直线斜率的...