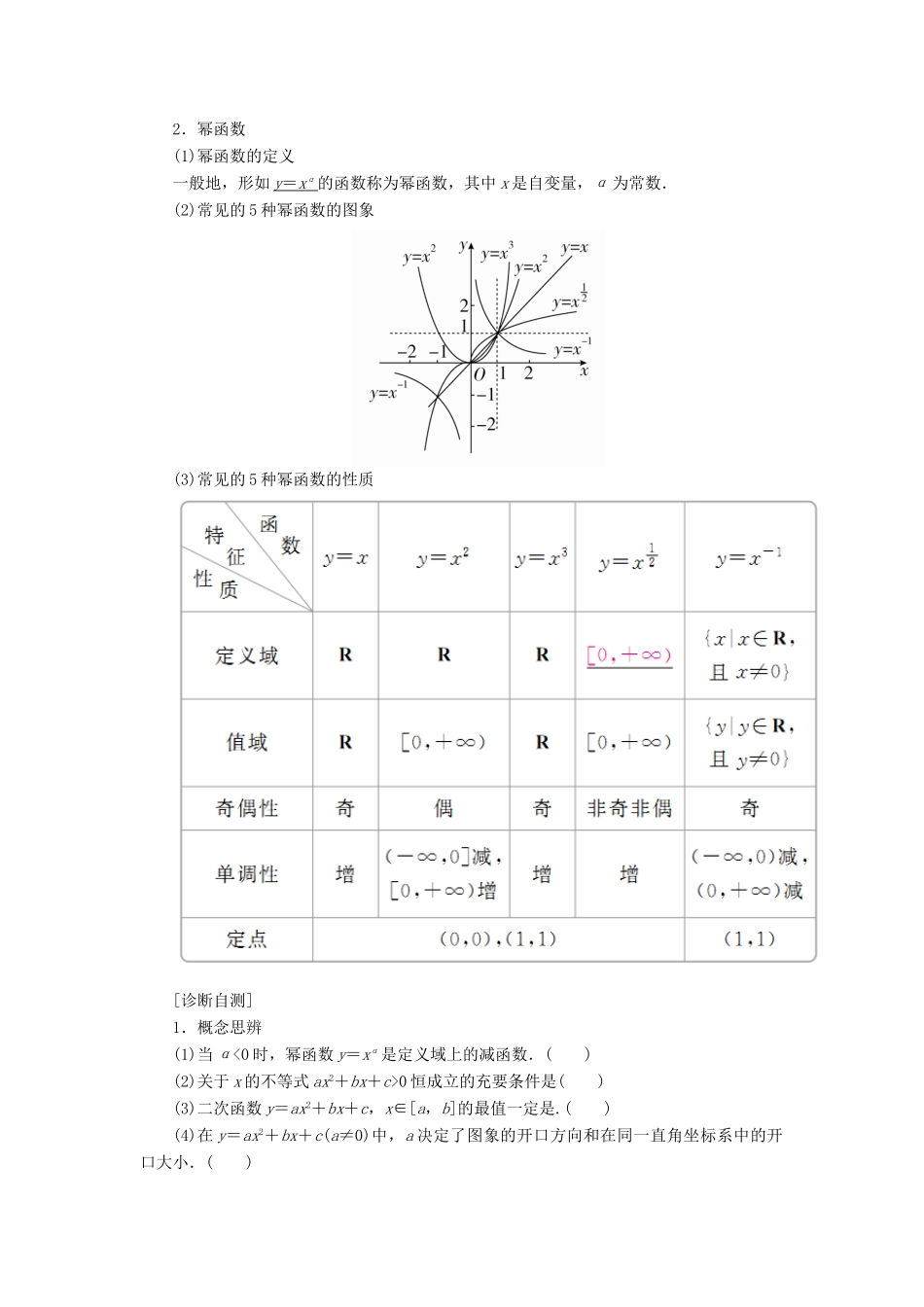
2.4 二次函数与幂函数[知识梳理]1.二次函数(1)二次函数解析式的三种形式① 一般式:f(x)=ax 2 + bx + c ( a ≠0) . ② 顶点式:f(x)=a ( x - m ) 2 + n ( a ≠0) . ③ 两根式:f(x)=a ( x - x 1)( x - x 2)( a ≠0) . (2)二次函数的图象和性质2.幂函数(1)幂函数的定义一般地,形如 y = x α 的函数称为幂函数,其中 x 是自变量,α 为常数.(2)常见的 5 种幂函数的图象(3)常见的 5 种幂函数的性质[诊断自测]1.概念思辨(1)当 α<0 时,幂函数 y=xα是定义域上的减函数.( )(2)关于 x 的不等式 ax2+bx+c>0 恒成立的充要条件是( )(3)二次函数 y=ax2+bx+c,x∈[a,b]的最值一定是.( )(4)在 y=ax2+bx+c(a≠0)中,a 决定了图象的开口方向和在同一直角坐标系中的开口大小.( )答案 (1)× (2)× (3)× (4)√ 2.教材衍化(1)(必修 A1P44T9)函数 y=(x2-3x+10)-1的递增区间是( )A.(-∞,-2)B.(5,+∞)C. D.答案 C解析 由于 x2-3x+10>0 恒成立,即函数的定义域为(-∞,+∞),设 t=x2-3x-10,则 y=t-1是(0,+∞)上的减函数,根据复合函数单调性的性质,要求函数 y=(x2-3x+10)-1的递增区间,即求 t=x2-3x+10 的单调递减区间, t=x2-3x+10 的单调递减区间是,则所求函数的递增区间为.故选 C.(2)(必修 A1P78探究) 若四个幂函数 y=xa,y=xb,y=xc,y=xd在同一坐标系中的图象如图,则 a,b,c,d 的大小关系是( )A.d>c>b>aB.a>b>c>dC.d>c>a>bD.a>b>d>c答案 B解析 幂函数 a=2,b=,c=-,d=-1 的图象,正好和题目所给的形式相符合,在第一象限内,x=1 的右侧部分的图象,图象由下至上,幂指数增大,所以 a>b>c>d.故选B.3.小题热身(1)(2017·济南诊断)已知幂函数 f(x)=k·xα的图象过点,则 k+α=( )A.B.1 C.D.2答案 C解析 由幂函数的定义知 k=1.又 f=,所以 α=,解得 α=,从而 k+α=.故选 C.(2)函数 f(x)=x2-ax-a 在[0,2]上的最大值为 1,则实数 a 等于( )A.-1B.1C.-2D.2答案 B解析 解法一:(分类讨论)当对称轴 x=≤1,即 a≤2 时,f(x)max=f(2)=4-3a=1,解得 a=1 符合题意;当 a>2 时,f(x)max=f(0)=-a=1,解得 a=-1(舍去).综上所述,实数 a=1.故选 B.解法二:(代入法)当 a=-1 时,f(x)=x2+x+1 在[0,2]上的...