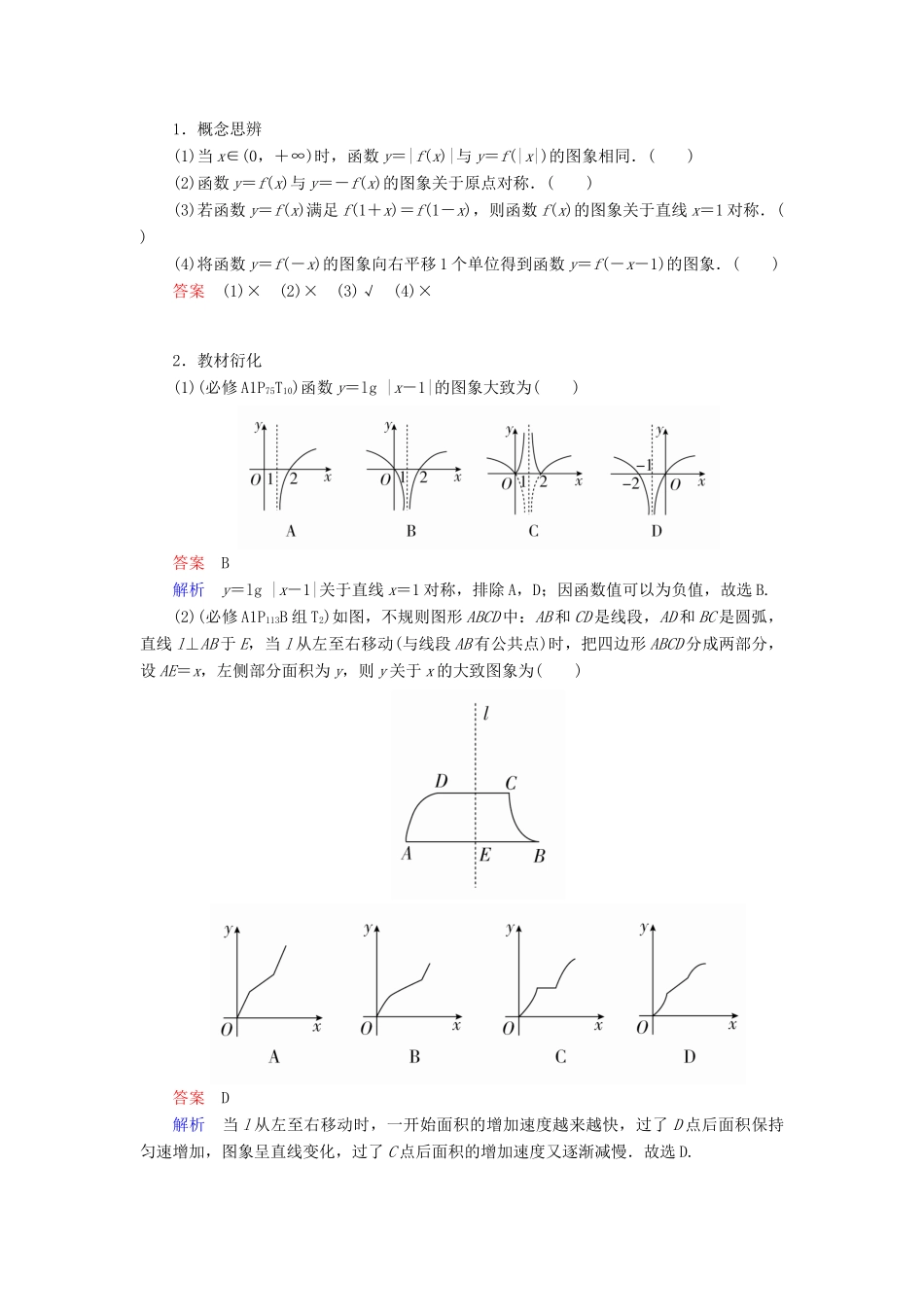
2.7 函数的图象 [知识梳理]1.利用描点法作函数图象的流程2.变换法作图(1)平移变换提醒:对于平移,往往容易出错,在实际判断中可熟记口诀:左加右减,上加下减.(2)对称变换①y=f(x)――→y=- f ( x ) ;②y=f(x)――→y=f ( - x ) ;③y=f(x)――→y=- f ( - x ) ;④y=ax(a>0 且 a≠1)――→y=logax ( a >0 且 a ≠1) . (3)翻折变换①y=f(x)――――――――――――――→y=|f(x)|;②y=f(x)――――――――――――――→y=f(|x|).(4)伸缩变换3.有关对称性的常用结论(1)函数图象自身的轴对称①f(-x)=f(x)⇔函数 y=f(x)的图象关于 y 轴对称;② 函数 y=f(x)的图象关于 x=a 对称⇔f(a+x)=f(a-x)⇔f(x)=f(2a-x)⇔f(-x)=f(2a+x);③ 若函数 y=f(x)的定义域为 R,且有 f(a+x)=f(b-x),则函数 y=f(x)的图象关于直线 x=对称.(2)函数图象自身的中心对称①f(-x)=-f(x)⇔函数 y=f(x)的图象关于原点对称;② 函数 y=f(x)的图象关于(a,0)对称⇔f(a+x)=-f(a-x)⇔f(x)=-f(2a-x)⇔f(-x)=-f(2a+x);③ 函数 y=f(x)的图象关于点(a,b)成中心对称⇔f(a+x)=2b-f(a-x)⇔f(x)=2b-f(2a-x);④ 若函数 y=f(x)定义域为 R,且满足条件 f(a+x)+f(b-x)=c(a,b,c 为常数),则函数 y=f(x)的图象关于点对称.(3)两个函数图象之间的对称关系① 函数 y=f(a+x)与 y=f(b-x)的图象关于直线 x=对称;函数 y=f(x)与 y=f(2a-x)的图象关于直线 x=a 对称;② 函数 y=f(x)与 y=2b-f(x)的图象关于直线 y=b 对称;③ 函数 y=f(x)与 y=2b-f(2a-x)的图象关于点(a,b)对称.[诊断自测]1.概念思辨(1)当 x∈(0,+∞)时,函数 y=|f(x)|与 y=f(|x|)的图象相同.( )(2)函数 y=f(x)与 y=-f(x)的图象关于原点对称.( )(3)若函数 y=f(x)满足 f(1+x)=f(1-x),则函数 f(x)的图象关于直线 x=1 对称.( )(4)将函数 y=f(-x)的图象向右平移 1 个单位得到函数 y=f(-x-1)的图象.( )答案 (1)× (2)× (3)√ (4)× 2.教材衍化(1)(必修 A1P75T10)函数 y=lg |x-1|的图象大致为( )答案 B解析 y=lg |x-1|关于直线 x=1 对称,排除 A,D;因函数值可以为负值,故选 B.(2)(必修 A1P113B 组 T2)如图,不规则图形 ABCD 中:AB 和 CD 是线段,AD 和 BC 是圆弧,直线 l⊥AB 于...