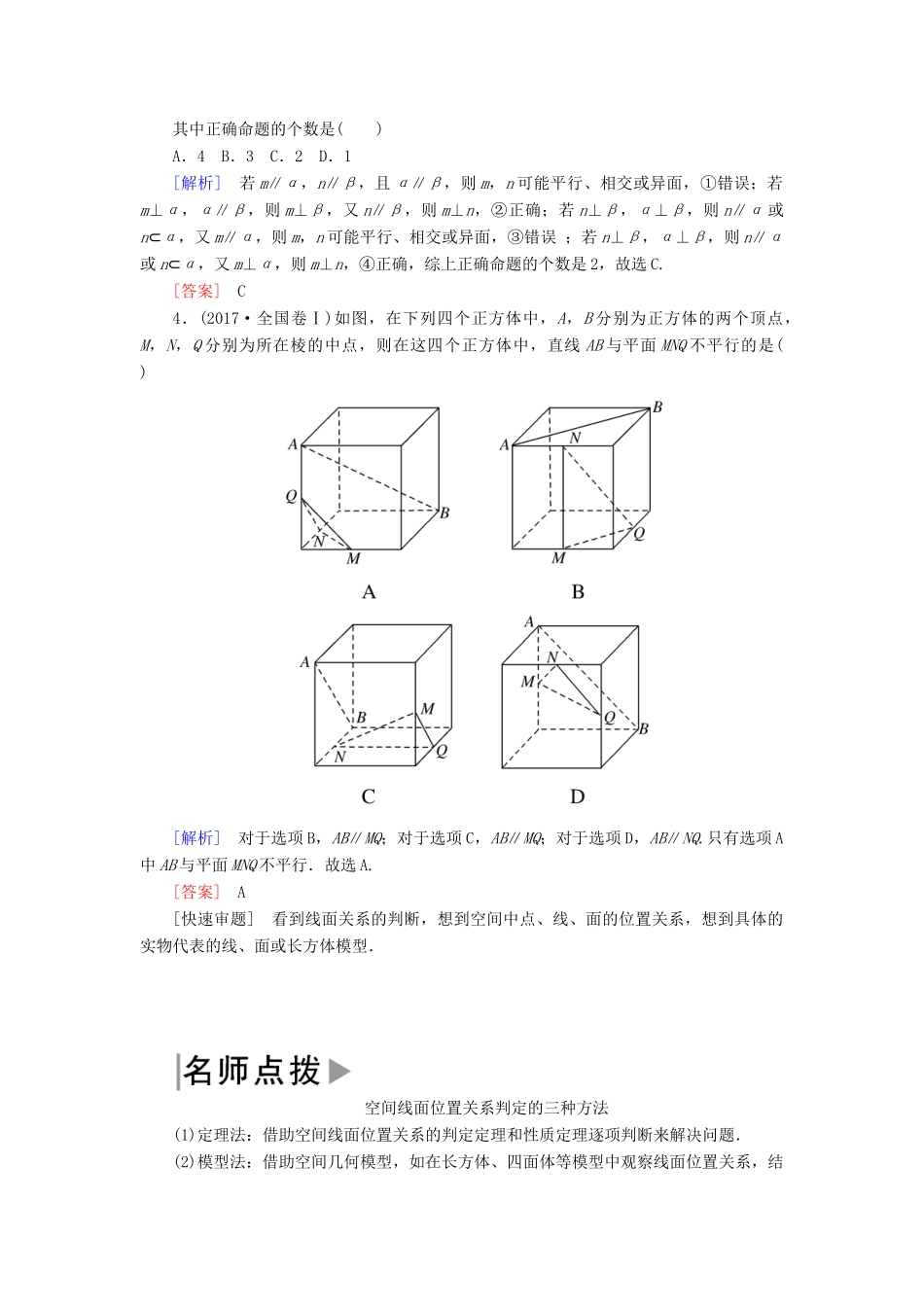
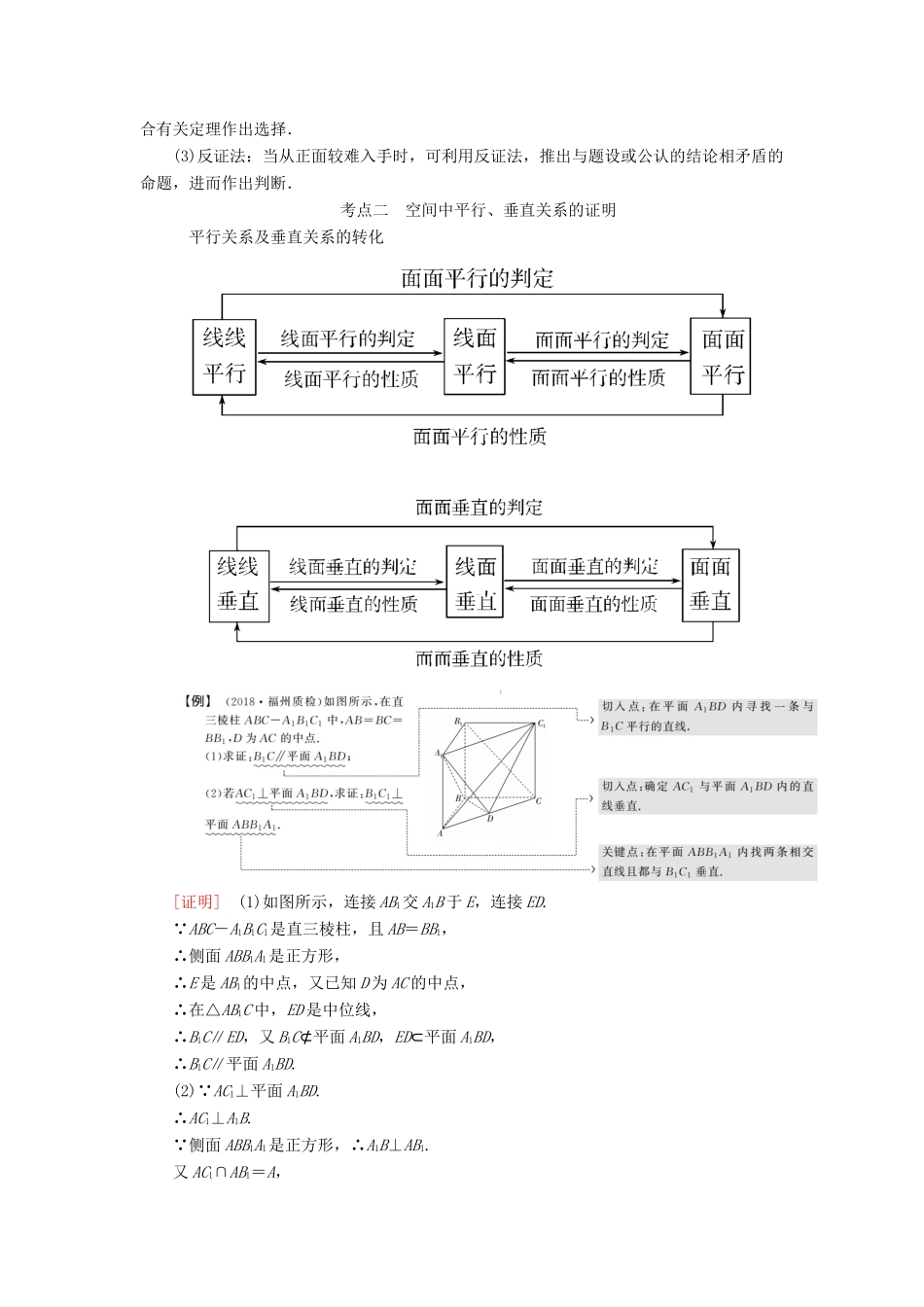
第二讲 点、直线、平面之间的位置关系考点一 空间线面位置关系的判断1.直线、平面平行的判定及其性质(1)线面平行的判定定理:a⊄α,b⊂α,a∥b,⇒a∥α.(2)线面平行的性质定理:a∥α,a⊂β,α∩β=b,⇒a∥b.(3)面面平行的判定定理:a⊂β,b⊂β,a∩b=P,a∥α,b∥α,⇒α∥β.(4)面面平行的性质定理:α∥β,α∩γ=a,β∩γ=b,⇒a∥b.2.直线、平面垂直的判定及其性质(1)线面垂直的判定定理:m⊂α,n⊂α,m∩n=P,l⊥m,l⊥n,⇒l⊥α.(2)线面垂直的性质定理:a⊥α,b⊥α,⇒a∥b.(3)面面垂直的判定定理:a⊂β,a⊥α,⇒α⊥β.(4)面面垂直的性质定理:α⊥β,α∩β=l,a⊂α,a⊥l,⇒a⊥β.[对点训练]1.(2018·安徽黄山二模)下列说法中,错误的是( )A.若平面 α∥平面 β,平面 α∩平面 γ=l,平面 β∩平面 γ=m,则 l∥mB.若平面 α⊥平面 β,平面 α∩平面 β=l,m⊂α,m⊥l,则 m⊥βC.若直线 l⊥平面 α,平面 α⊥平面 β,则 l∥βD.若直线 l∥平面 α,平面 α∩平面 β=m,直线 l⊂平面 β,则 l∥m[解析] 对于 A,由面面平行的性质定理可知为真命题,故 A 正确;对于 B,由面面垂直的性质定理可知为真命题,故 B 正确;对于 C,若 l⊥α,α⊥β,则 l∥β 或 l⊂β,故 C 错误;对于 D,由线面平行的性质定理可知为真命题,故 D 正确.综上,选 C.[答案] C2.(2018·湖北重点中学联考)设 m,n 是平面 α 内的两条不同直线,l1,l2是平面 β内两条相交直线,则 α⊥β 的一个充分不必要条件是( )A.l1⊥m,l1⊥n B.m⊥l1,m⊥l2C.m⊥l1,n⊥l2 D.m∥n,l1⊥n[解析] 由 m⊥l1,m⊥l2 及已知条件可得 m⊥β,又 m⊂α,所以 α⊥β;反之,α⊥β 时未必有 m⊥l1,m⊥l2,故“m⊥l1,m⊥l2”是“α⊥β”的充分不必要条件,其余选项均推不出 α⊥β,故选 B.[答案] B3.(2018·潍坊模拟)已知两条不同的直线 m,n 和两个不同的平面 α,β,以下四个命题:① 若 m∥α,n∥β,且 α∥β,则 m∥n;② 若 m⊥α,n∥β,且 α∥β,则 m⊥n;③ 若 m∥α,n⊥β,且 α⊥β,则 m∥n;④ 若 m⊥α,n⊥β,且 α⊥β,则 m⊥n.其中正确命题的个数是( )A.4 B.3 C.2 D.1[解析] 若 m∥α,n∥β,且 α∥β,则 m,n 可能平行、相交或异面,①错误;若m⊥α,α∥β,则 m⊥β,又 n∥...