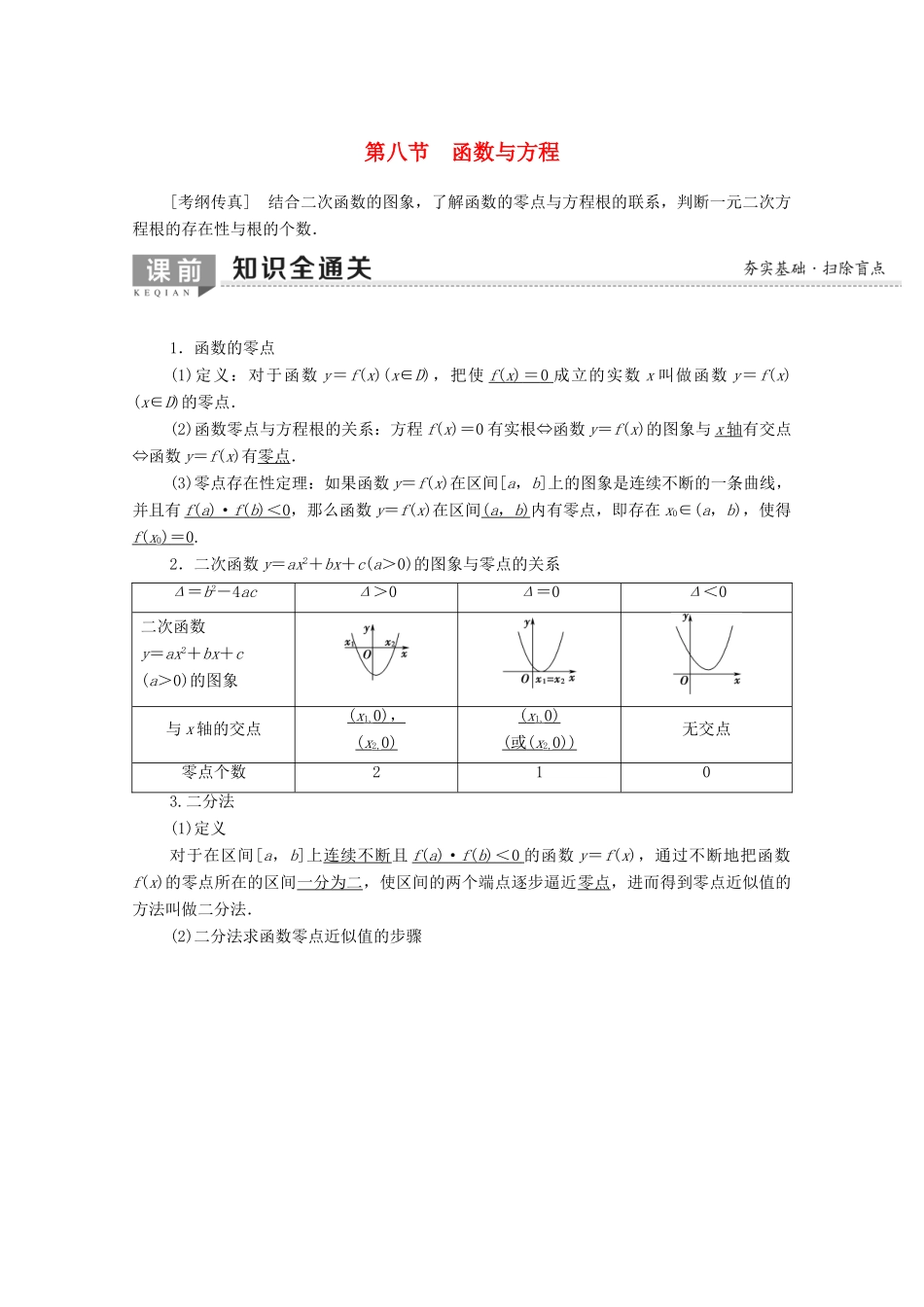
第八节 函数与方程[考纲传真] 结合二次函数的图象,了解函数的零点与方程根的联系,判断一元二次方程根的存在性与根的个数.1.函数的零点(1)定义:对于函数 y=f(x)(x∈D),把使 f ( x ) = 0 成立的实数 x 叫做函数 y=f(x)(x∈D)的零点.(2)函数零点与方程根的关系:方程 f(x)=0 有实根⇔函数 y=f(x)的图象与 x 轴 有交点⇔函数 y=f(x)有零点.(3)零点存在性定理:如果函数 y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有 f ( a )· f ( b ) < 0 ,那么函数 y=f(x)在区间( a , b ) 内有零点,即存在 x0∈(a,b),使得f ( x 0) = 0 .2.二次函数 y=ax2+bx+c(a>0)的图象与零点的关系Δ=b2-4acΔ>0Δ=0Δ<0二次函数y=ax2+bx+c(a>0)的图象与 x 轴的交点( x 1,0) , ( x 2,0)( x 1,0)( 或 ( x 2,0))无交点零点个数2103.二分法(1)定义对于在区间[a,b]上连续不断且 f ( a )· f ( b ) < 0 的函数 y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.(2)二分法求函数零点近似值的步骤[常用结论]1.函数 f(x)在区间[a,b]上的图象是连续不断的曲线,则“f(a)·f(b)<0”是函数f(x)在区间(a,b)内有零点的充分不必要条件.2.若函数 f(x)在区间[a,b]上是单调函数,且 f(a)·f(b)<0,则函数 f(x)在区间(a,b)内只有一个零点.[基础自测]1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)函数的零点就是函数的图象与 x 轴的交点.( )(2)函数 y=f(x),x∈D 在区间(a,b)⊆D 内有零点(函数图象连续不断),则 f(a)·f(b)<0.( )(3)若函数 f(x)在(a,b)上单调且 f(a)·f(b)<0,则函数 f(x)在[a,b]上有且只有一个零点.( )(4)二次函数 y=ax2+bx+c 在 b2-4ac<0 时没有零点.( )[答案] (1)× (2)× (3)× (4)√2.(教材改编)函数 f(x)=ex+3x 的零点个数是( )A.0 B.1 C.2 D.3B [ f(-1)=-3<0,f(0)=1>0,∴f(x)在(-1,0)内有零点,又 f(x)为增函数,∴函数 f(x)有且只有一个零点.]3.下列函数中,既是偶函数又存在零点的是( )A.y=cos x B.y=sin xC.y=ln x D.y=x2+1A [由于 y=sin x 是奇函数,y=ln x 是非奇非偶函数,y=x2+1 是偶函数但没有零点,只有 y=cos x ...