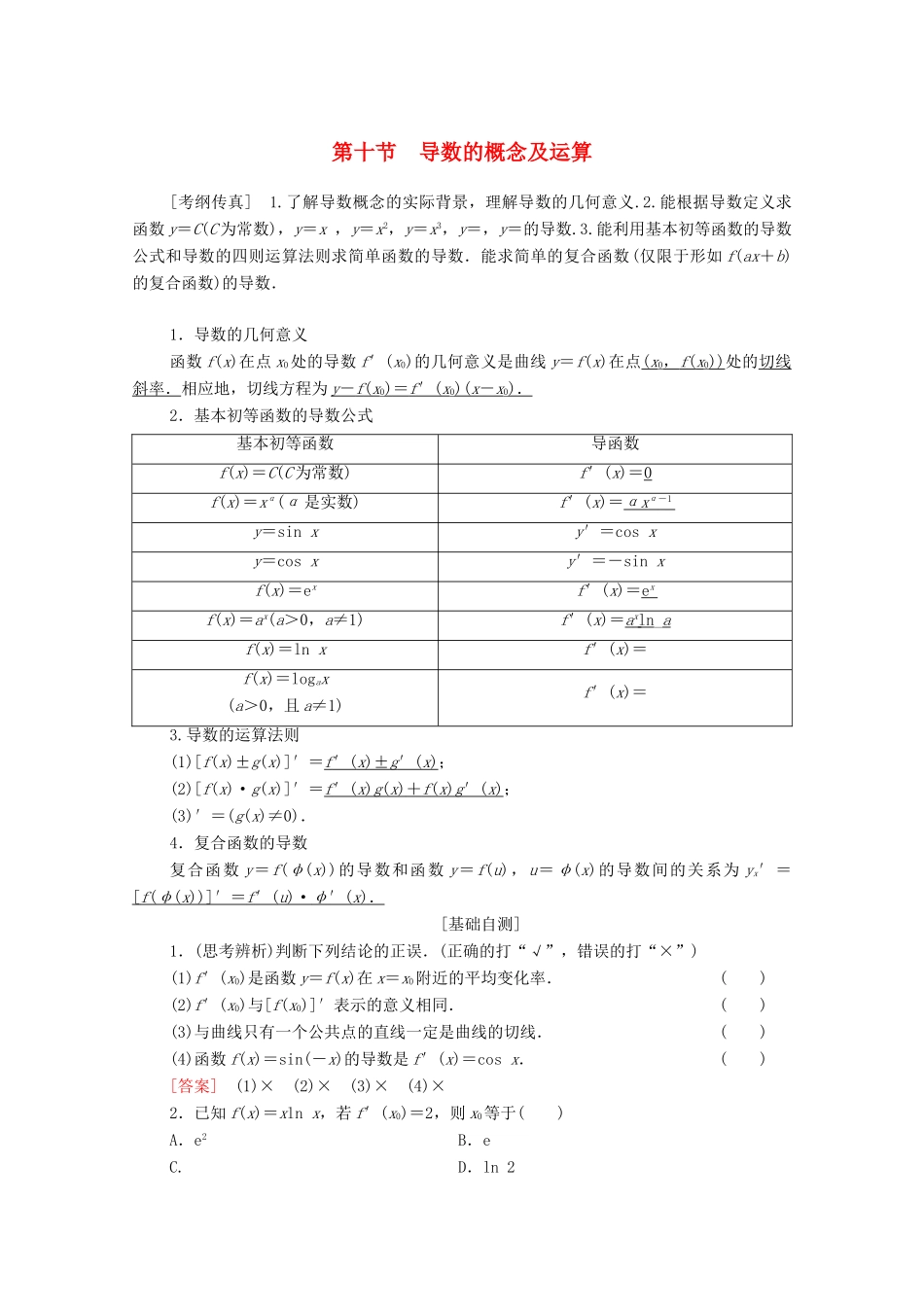
第十节 导数的概念及运算[考纲传真] 1.了解导数概念的实际背景,理解导数的几何意义.2.能根据导数定义求函数 y=C(C 为常数),y=x ,y=x2,y=x3,y=,y=的导数.3.能利用基本初等函数的导数公式和导数的四则运算法则求简单函数的导数.能求简单的复合函数(仅限于形如 f(ax+b)的复合函数)的导数.1.导数的几何意义函数 f(x)在点 x0处的导数 f′(x0)的几何意义是曲线 y=f(x)在点( x 0, f ( x 0))处的切线斜率.相应地,切线方程为 y - f ( x 0) = f ′( x 0)( x - x 0) . 2.基本初等函数的导数公式基本初等函数导函数f(x)=C(C 为常数)f′(x)=0f(x)=xα(α 是实数)f′(x)=αx α - 1 y=sin xy′=cos xy=cos xy′=-sin xf(x)=exf′(x)=e x f(x)=ax(a>0,a≠1)f′(x)=a x ln _af(x)=ln xf′(x)=f(x)=logax(a>0,且 a≠1)f′(x)=3.导数的运算法则(1)[f(x)±g(x)]′=f ′( x )± g ′( x ) ;(2)[f(x)·g(x)]′=f ′( x ) g ( x ) + f ( x ) g ′( x ) ;(3)′=(g(x)≠0).4.复合函数的导数复合函数 y=f(φ(x))的导数和函数 y=f(u),u=φ(x)的导数间的关系为 yx′=[ f ( φ ( x ))]′ = f ′( u )· φ ′( x ) . [基础自测]1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)f′(x0)是函数 y=f(x)在 x=x0附近的平均变化率.( )(2)f′(x0)与[f(x0)]′表示的意义相同.( )(3)与曲线只有一个公共点的直线一定是曲线的切线.( )(4)函数 f(x)=sin(-x)的导数是 f′(x)=cos x.( )[答案] (1)× (2)× (3)× (4)×2.已知 f(x)=xln x,若 f′(x0)=2,则 x0等于( )A.e2 B.eC. D.ln 2B [ f′(x)=ln x+x·=ln x+1,由 f′(x0)=ln x0+1=2 得 ln x0=1,∴x0=e.]3.有一机器人的运动方程为 s(t)=t2+(t 是时间,s 是位移),则该机器人在时刻 t=2时的瞬时速度为( )A. B. C. D.D [由题意知,机器人的速度方程为 v(t)=s′(t)=2t-,故当 t=2 时,机器人的瞬时速度为 v(2)=2×2-=.]4.曲线 y=x2+在点(1,2)处的切线方程为________.x-y+1=0 [ y′=2x-,∴y′|x=1=1,即曲线在点(1,2)处的切线的斜率 k=1,∴切线方程为 y-2=x-1,即 x-y+1=0.]5.设 f(x)=ln(3-2x)+cos 2x,则 f′(0)=________.- ...