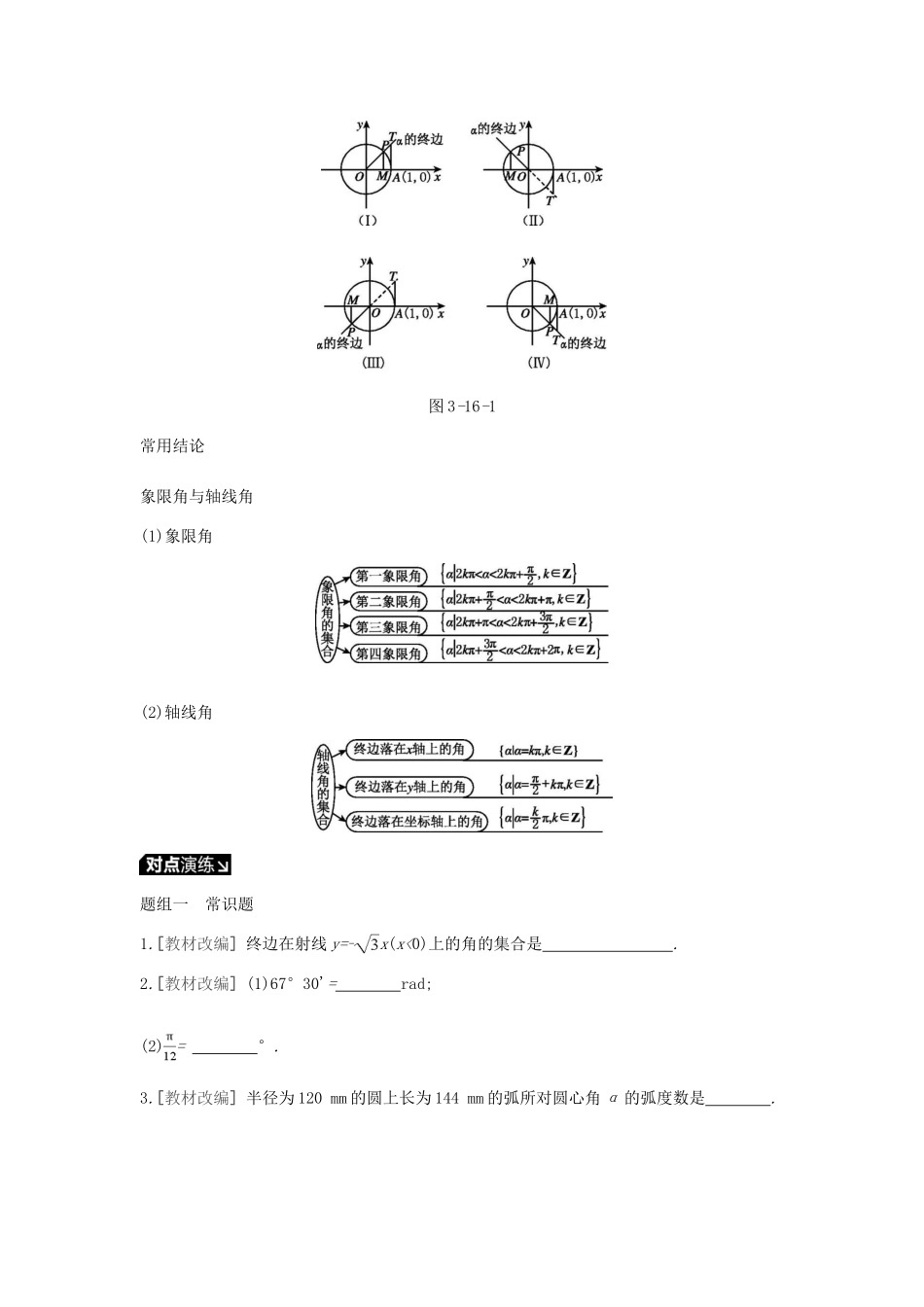
第三单元 三角函数、解三角形第 16 讲 任意角和弧度制及任意角的三角函数课前双击巩固1.角的概念的推广(1)定义:角可以看成平面内的一条射线绕着 从一个位置旋转到另一个位置所形成的图形. (2)分类:按旋转方向分为 、 和零角;按终边位置分为 和轴线角. (3)终边相同的角:所有与角 α 终边相同的角,连同角 α 在内,构成的角的集合是 S= . 2.弧度制的定义和公式(1)定义:把长度等于 的弧所对的圆心角叫作 1 弧度的角.弧度记作 rad. (2)公式:角 α 的弧度数的绝对值|α|= (弧长用 l 表示)角度与弧度的换算①1°= rad,②1 rad=°弧长公式弧长 l= 扇形面积公式S= lr= |α|r23.任意角的三角函数(1)定义:设 α 是一个任意角,它的终边与单位圆交于点 P(x,y),则 sin α= ,cos α= ,tan α= (x≠0). (2)几何表示(单位圆中的三角函数线):图 3-16-1 中的有向线段 OM,MP,AT 分别称为角 α 的 、 和 . 图 3-16-1常用结论象限角与轴线角(1)象限角(2)轴线角题组一 常识题1.[教材改编] 终边在射线 y=-x(x<0)上的角的集合是 . 2.[教材改编] (1)67°30'= rad; (2) = °. 3.[教材改编] 半径为 120 mm 的圆上长为 144 mm 的弧所对圆心角 α 的弧度数是 . 4.[教材改编] 若角 α 的终边经过点 P(-1,2),则 sin α-cos α+tan α= . 题组二 常错题◆索引:对角的范围把握不准;由值求角时没有注意角的范围;求三角函数值时没有考虑角的终边所在的象限;求弧长或者扇形面积把角化为弧度数时出错.5.在△ABC 中,若 sin A=,则 A= . 6.已知点 P(sin α-cos α,tan α)在第二象限,则在[0,2π]内 α 的取值范围是 . 7.已知角 α 的终边落在直线 y=-3x 上,则-= . 8.若一扇形的圆心角为 72°,半径为 20 cm,则扇形的面积为 cm2. 课堂考点探究探究点一 角的集合表示及象限角的判定1 (1)设集合 M= x x= ·180°+45°,k∈Z ,N= x x= ·180°+45°,k∈Z ,那么( )A.M=NB.M⊆NC.N⊆MD.M∩N=⌀ (2)已知角 α 的终边在图 3-16-2 中阴影部分表示的范围内(不包括边界),则所有角 α 构成的集合是 . 图 3-16-2[总结反思] 把角表示成 2 k π +α ( k ∈ Z,0 ≤ α< 2π) 的形式,即可判断其所在的象限.式题 (1)已知角 α,β 的终边关于直线 x+y=0 对称,且 α=-60°,则 β= . (2)若角 α 的终边在 x 轴的上方,则 是第 象限角. 探究点...