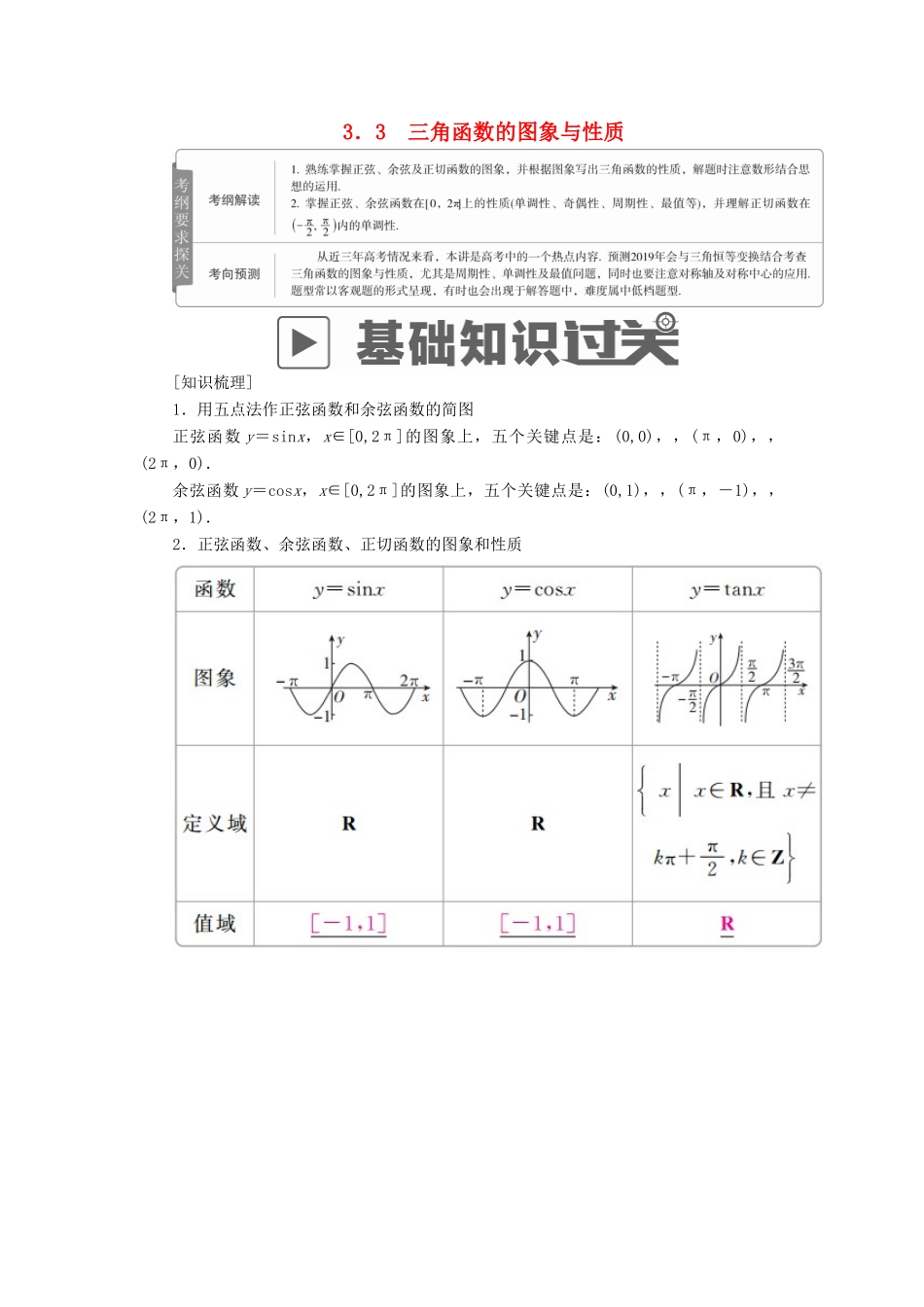
3.3 三角函数的图象与性质[知识梳理]1.用五点法作正弦函数和余弦函数的简图正弦函数 y=sinx,x∈[0,2π]的图象上,五个关键点是:(0,0),,(π,0),,(2π,0).余弦函数 y=cosx,x∈[0,2π]的图象上,五个关键点是:(0,1),,(π,-1),,(2π,1).2.正弦函数、余弦函数、正切函数的图象和性质[诊断自测]1.概念思辨(1)y=tanx 在整个定义域上是增函数.( )(2)函数 f(x)=sin(-2x)与 f(x)=sin2x 的单调增区间都是(k∈Z).( )(3)由 sin=sin 知,是正弦函数 y=sinx(x∈R)的一个周期.( )(4)若非零实数 T 是函数 f(x)的周期,则 kT(k 是非零整数)也是函数 f(x)的周期.( )答案 (1)× (2)× (3)× (4)√2.教材衍化(1)(必修 A4P46T2)函数 f(x)=(1+tanx)cosx 的最小正周期、最大值为( )A.2π,2 B., C.π,2 D.,答案 A解析 f(x)=(1+tanx)cosx=·cosx=2cos,则 T=2π.最大值为 2.故选 A.(2)(必修 A4P40T4)已知函数 f(x)=sin(x∈R),下列结论错误的是( )A.函数 f(x)是偶函数B.函数 f(x)的最小正周期为 πC.函数 f(x)在区间上是增函数D.函数 f(x)的图象关于直线 x=对称答案 D解析 f(x)=sin=-cos2x,此函数为最小正周期为 π 的偶函数,所以 A、B 正确.由函数 y=cosx 的单调性知 C 正确.函数图象的对称轴方程为 x=(k∈Z),显然,无论 k 取任何整数,x≠,所以 D 错误.故选 D.3.小题热身(1)函数 f(x)=sin 在区间上的最小值为( )A.-1 B.- C. D.0答案 B解析 由已知 x∈,得 2x-∈,所以 sin∈,故函数 f(x)=sin 在区间上的最小值为-.故选 B.(2)函数 y=tan 的单调递增区间是________,最小正周期是________.答案 (k∈Z) 2π解析 由 kπ-<+,由正弦曲线得+2kπ1,即 a>2,...