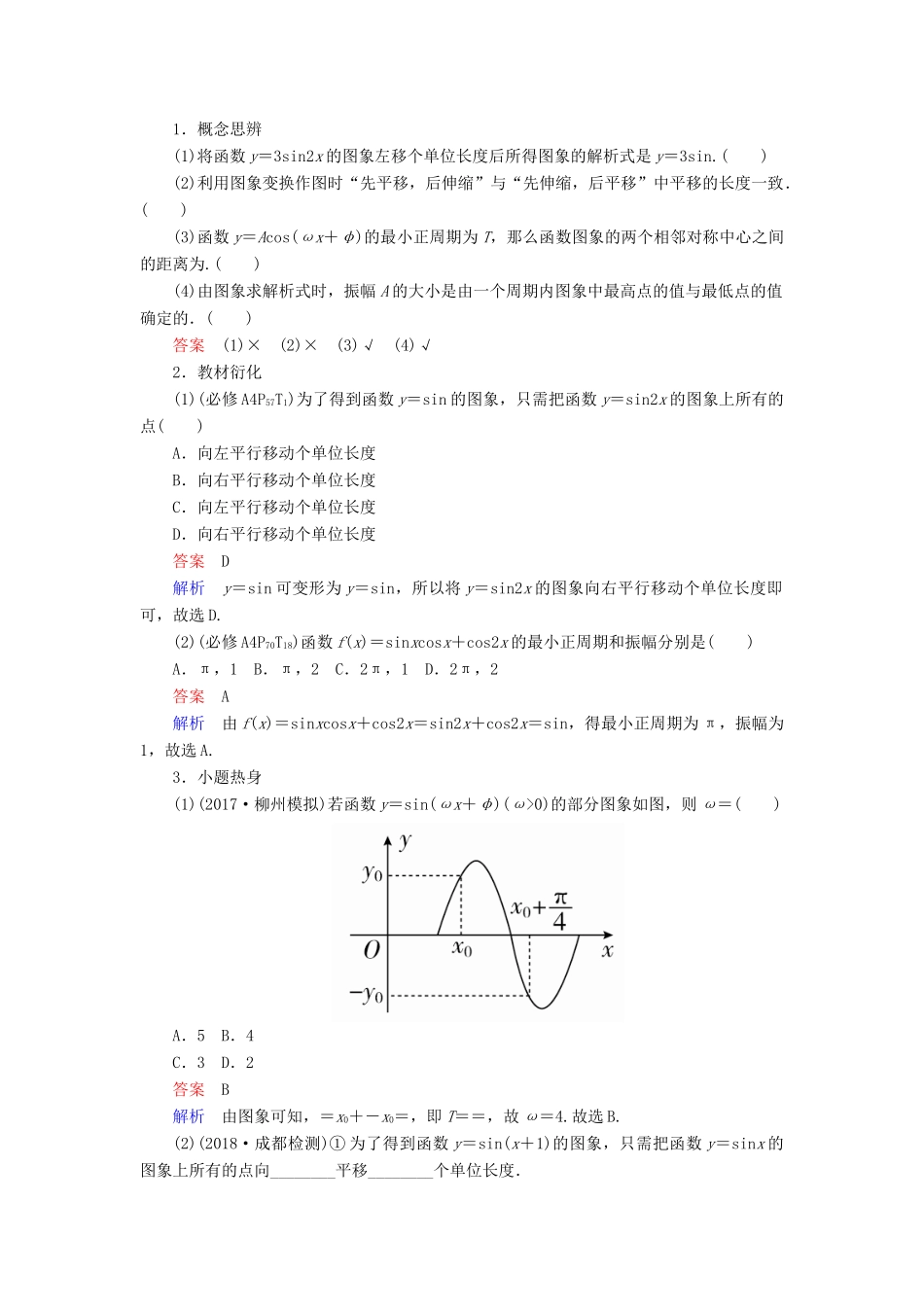
3.4 函数 y=Asin(ωx+φ)的图象及应用[知识梳理]1.“五点法”作函数 y=Asin(ωx+φ)(A>0,ω>0)的简图“五点法”作图的五点是在一个周期内的最高点、最低点及与 x 轴相交的三个点,作图时的一般步骤为:(1)定点:如下表所示.(2)作图:在坐标系中描出这五个关键点,用平滑的曲线顺次连接得到 y=Asin(ωx+φ)在一个周期内的图象.(3)扩展:将所得图象,按周期向两侧扩展可得 y=Asin(ωx+φ)在 R 上的图象.2.函数 y=sinx 的图象经变换得到 y=Asin(ωx+φ)(A>0,ω>0)的图象的步骤如下:[诊断自测]1.概念思辨(1)将函数 y=3sin2x 的图象左移个单位长度后所得图象的解析式是 y=3sin.( )(2)利用图象变换作图时“先平移,后伸缩”与“先伸缩,后平移”中平移的长度一致.( )(3)函数 y=Acos(ωx+φ)的最小正周期为 T,那么函数图象的两个相邻对称中心之间的距离为.( )(4)由图象求解析式时,振幅 A 的大小是由一个周期内图象中最高点的值与最低点的值确定的.( )答案 (1)× (2)× (3)√ (4)√2.教材衍化(1)(必修 A4P57T1)为了得到函数 y=sin 的图象,只需把函数 y=sin2x 的图象上所有的点( )A.向左平行移动个单位长度B.向右平行移动个单位长度C.向左平行移动个单位长度D.向右平行移动个单位长度答案 D解析 y=sin 可变形为 y=sin,所以将 y=sin2x 的图象向右平行移动个单位长度即可,故选 D.(2)(必修 A4P70T18)函数 f(x)=sinxcosx+cos2x 的最小正周期和振幅分别是( )A.π,1 B.π,2 C.2π,1 D.2π,2答案 A解析 由 f(x)=sinxcosx+cos2x=sin2x+cos2x=sin,得最小正周期为 π,振幅为1,故选 A.3.小题热身(1)(2017·柳州模拟)若函数 y=sin(ωx+φ)(ω>0)的部分图象如图,则 ω=( )A.5 B.4C.3 D.2答案 B解析 由图象可知,=x0+-x0=,即 T==,故 ω=4.故选 B.(2)(2018·成都检测)① 为了得到函数 y=sin(x+1)的图象,只需把函数 y=sinx 的图象上所有的点向________平移________个单位长度.② 为了得到函数 y=sin(2x+1)的图象,只需把函数 y=sin2x 的图象上所有的点向________平移________个单位长度.答案 ①左 1 ②左 题型 1 函数 y=Asin(ωx+φ)的图象\s\up7( ) (2015·湖北高考)某同学用“五点法”画函数 f(x)=Asin(ωx+φ)在某一个周期内的图象时,列表并填入了部分数据,如下表:(1)请将上表数据补充...