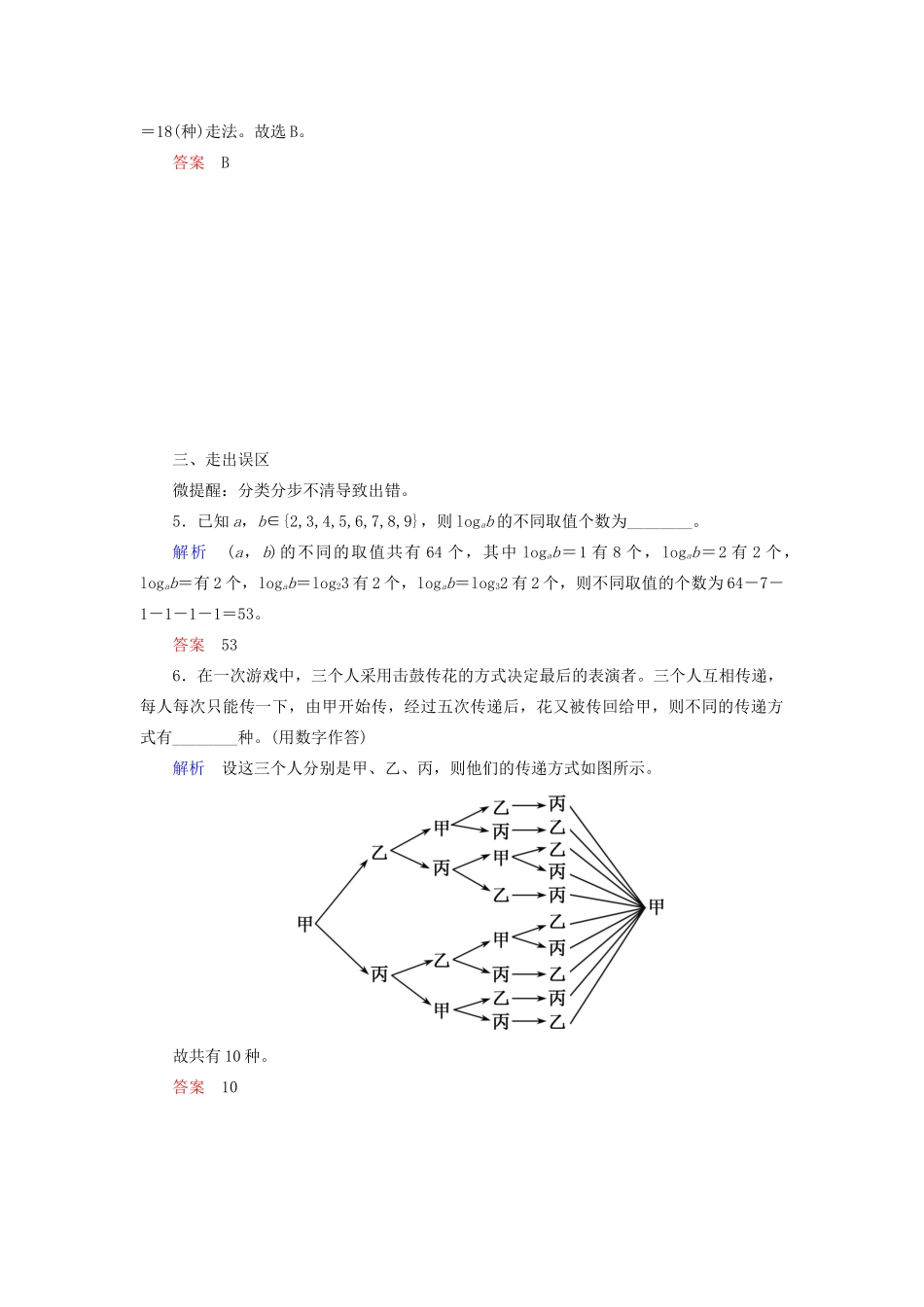
第一节 两个计数原理2019 考纲考题考情两个计数原理完成一件事的策略完成这件事共有的方法分类加法计数原理有 n 类不同方案:在第 1 类方案中有 m1种不同的方法,在第 2 类方案中有 m2种不同的方法,…,在第 n类中有 mn种不同方法N=m1+ m 2+…+ m n 种不同的方法分步乘法计数原理需要 n 个步骤:做第 1 步有 m1种不同的方法,做第 2 步有 m2种不同的方法,…,做第 n 步有 mn种不同方法N=m1· m 2·…· m n 种不同的方法1.两个不同点(1)分类问题中的每一个方法都能完成这件事。(2)分步问题中每步的每一个方法都只能完成这件事的一部分。2.三个注意点(1)应用两个计数原理首先要弄清楚先分类还是先分步。(2)分类要做到“不重不漏”,正确把握分类标准。(3)分步要做到“步骤完整”,步步相连。一、走进教材1.(选修 2-3P5例 3 改编)书架的第 1 层放有 10 本不同的语文书,第 2 层放有 12 本不同的数学书,第 3 层放有 10 本不同的英语书,从书架中任取一本书,则不同的取法种数为( )A.32 B.100 C.120 D.1 200解析 有三类方法,第 1 类从第 1 层取 1 本语文书,有 10 种方法;第 2 类从第 2 层取1 本数学书,有 12 种方法;第 3 类从第 3 层取 1 本英语书,有 10 种方法,由分类加法计数原理,共有 10+12+10=32 种不同的取法。故选 A。答案 A2.(选修 2-3P10练习 T4改编)已知某公园有 4 个门,从一个门进,另一个门出,则不同的走法的种数为( )A.16 B.13 C.12 D.10解析 由分步乘法计数原理可知,走法总数为 4×3=12。故选 C。答案 C3.(选修 2-3P12A 组 T2改编)如图,从 A 城到 B 城有 3 条路;从 B 城到 D 城有 4 条路;从 A 城到 C 城有 4 条路,从 C 城到 D 城有 5 条路,则某旅客从 A 城到 D 城共有________条不同的路线。解析 不同路线共有 3×4+4×5=32(条)。答案 32二、走近高考4.(2016·全国卷Ⅱ)如图,小明从街道的 E 处出发,先到 F 处与小红会合,再一起到位于 G 处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为 ( )A.24 B.18 C.12 D.9解析 由 E 到 F 有 6 种走法,由 F 到 G 有 3 种走法,由分步乘法计数原理知,共 6×3=18(种)走法。故选 B。答案 B三、走出误区微提醒:分类分步不清导致出错。5.已知 a,b∈{2,3...