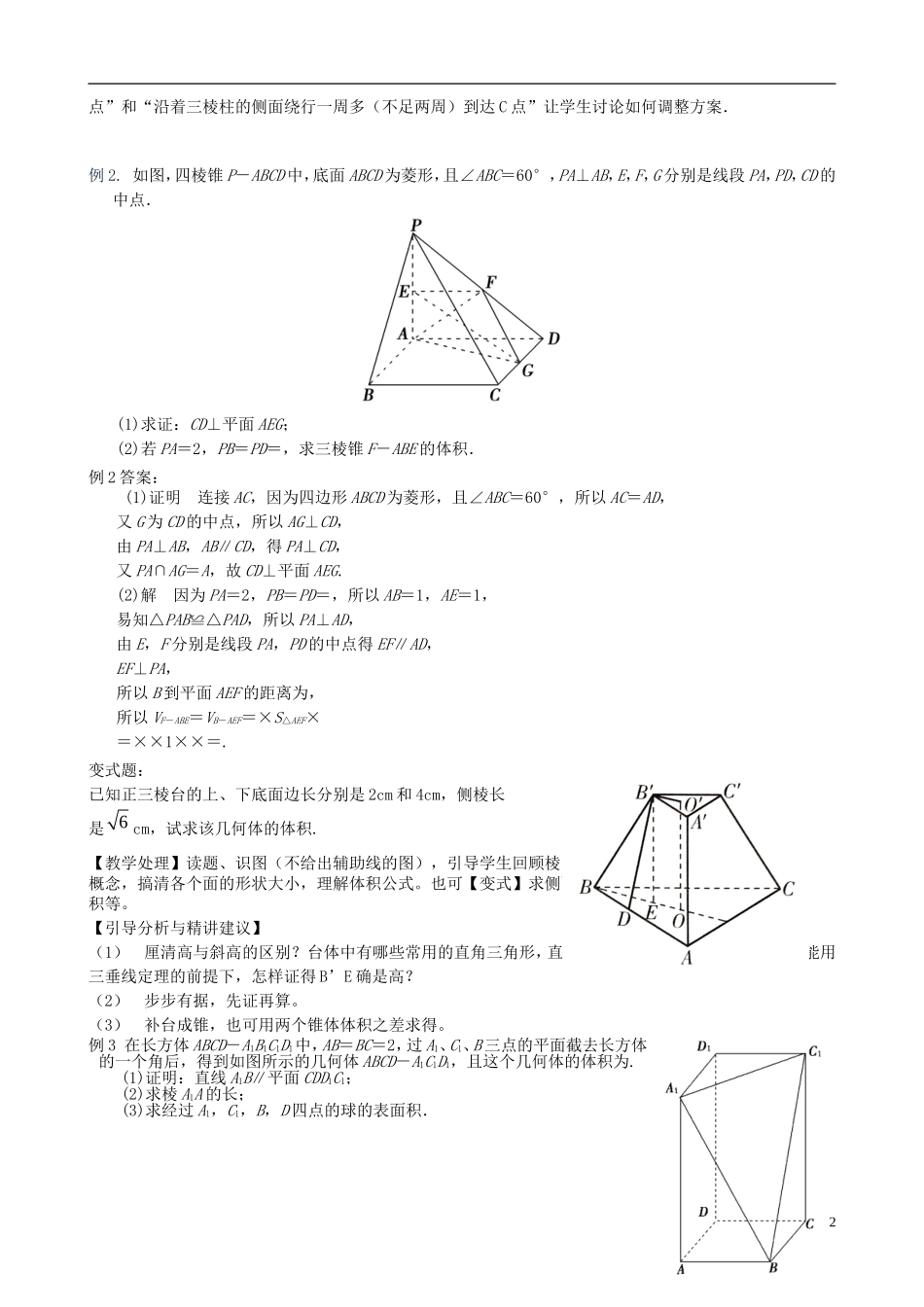
柱、锥、台、球的表面积和体积一、教学目标能运用公式求柱、锥、台、球的表面积和体积.二、知识梳理【回顾】 阅读课本必修 2 第 47 页至 59 页,理解以下内容.正棱柱、正棱锥、正棱台的侧面积公式及其关系;圆柱、圆锥、圆台的体积公式及其关系;柱体、锥体、台体的体积公式及其关系;球的表面积、体积公式.三、诊断练习1、教学处理:课前由学生自主完成 4 道小题,并要求将解题过程扼要地写在学习笔记栏。课前抽查批阅部分同学的解答,了解学生的思路及主要错误。找出学生错误的原因,设计“问题串”,将知识问题化,通过问题驱动,使教学言而有物,帮助学生内化知识,初步形成能力。点评时要简洁,要点击要害。2、诊断练习点评题 1.若圆锥的侧面积为 2,底面积为 ,则该圆锥的体积为__________.【分析与点评】本题是容易题,主要是考查圆锥侧面积公式和体积公式的正确使用.题 2.如图,已知一个多面体的平面展开图由一个边长为 1 的正方形和 4 个边长为 1 的正三角形组成,则该多面体的体积是__________.【分析与点评】该多面体是正四棱锥,侧棱长为 1,底面正方形外接圆的半径等于,由侧棱、底面正方形外接圆半径及高之间关系求解.题 3.正方体 ABCD—A1B1C1D1的棱长为,则四面体 AB1CD1的外接球的体积为__________.【分析与点评】正方体外接球半径是正方体棱长的倍得到球的半径求解. 四面体的外接球就是该正方体的外接球变式 1:棱长分别是 2,3,4 的长方体外接球的体积是________.变式 2:棱长都是 2 的正四面体的外接球的表面积为________.题 4. 已知三棱锥 S-ABC 的所有顶点都在球 O 的球面上,△ABC 是边长为 1 的正三角形,SC 为球 O 的直径,且 SC=2,则此棱锥的体积为_______【分析与点评】:在直角三角形 ASC 中,AC=1,∠SAC=90°,SC=2,∴SA==;同理 SB=.过 A 点作 SC的垂线交 SC 于 D 点,连接 DB,因△SAC≌△SBC,故 BD⊥SC,故 SC⊥平面 ABD,且平面 ABD 为等腰三角形,因∠ASC=30°,故 AD=SA=,则△ABD 的面积为×1× =,则三棱锥的体积为××2=.3、要点归纳(1)注意各个公式的推导过程,不要死记硬背公式本身,要熟悉柱体中的矩形、锥体中的直角三角形、台体中的直角梯形等特征图形在公式推导中的作用.(2)如果不是正棱柱、正棱锥、正棱台,在求其侧面积或全面积时,应对每一个侧面分别求解后再相加.(3)注意求体积的一此特殊方...