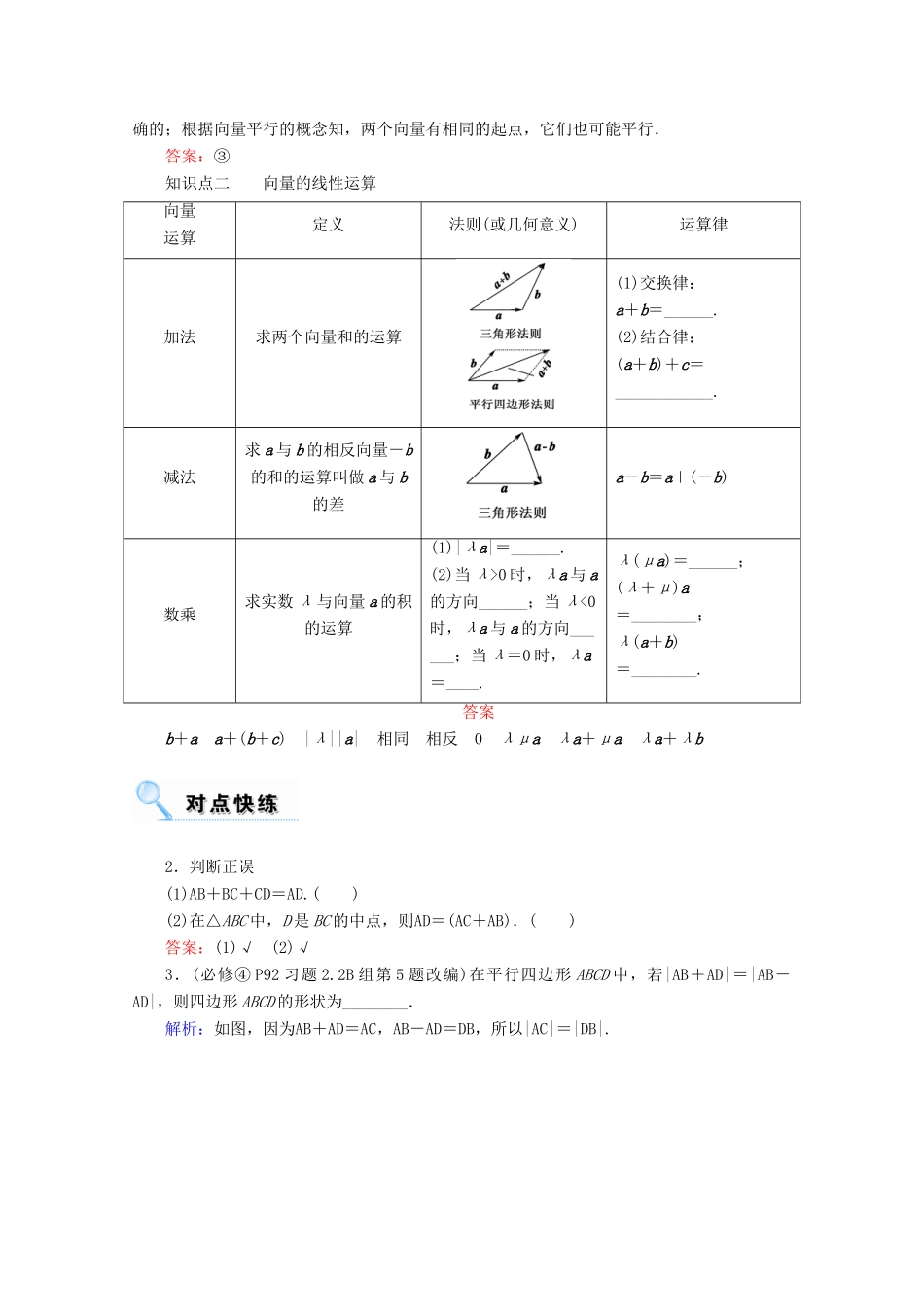
\s\up7(第一节) \s\up7(平面向量的概念及其线性运算) 1.了解向量的实际背景.2.理解平面向量的概念,理解两个向量相等的含义.3.理解向量的几何表示.4.掌握向量加法、减法的运算,并理解其几何意义.5.掌握向量数乘的运算及其几何意义,理解两个向量共线的含义.6.了解向量线性运算的性质及其几何意义.知识点一 向量的有关概念 1.向量:既有大小又有______的量叫做向量,向量的大小叫做向量的____.2.零向量:长度为____的向量,其方向是任意的.3.单位向量:长度等于________的向量.4.平行向量:方向相同或______的非零向量,又叫共线向量.规定:0 与任一向量共线.5.相等向量:长度相等且方向______的向量.6.相反向量:长度相等且方向______的向量.答案1.方向 模 2.0 3.1 个单位4.相反 5.相同 6.相反1.给出下列结论:① a 与 b 共线,b 与 c 共线,则 a 与 c 也共线;② 任意两个相等的非零向量的始点与终点是一个平行四边形的四个顶点;③ 向量 a 与 b 不共线,则 a 与 b 都是非零向量;④ 有相同起点的两个非零向量不平行.其中正确结论的序号是 ________.解析:结论①中的向量 b 如果是零向量,则结论不成立;结论②中两个向量的起点和终点在同一条直线上时,它们的起点和终点不是平行四边形的四个顶点;在结论③中,如果向量 a 与 b 中至少有一个零向量,根据零向量与任意向量共线,则 a 与 b 共线,故结论③是正确的;根据向量平行的概念知,两个向量有相同的起点,它们也可能平行.答案:③知识点二 向量的线性运算 向量运算定义法则(或几何意义)运算律加法求两个向量和的运算(1)交换律:a+b=______.(2)结合律:(a+b)+c=____________.减法求 a 与 b 的相反向量-b的和的运算叫做 a 与 b的差a-b=a+(-b)数乘求实数 λ 与向量 a 的积的运算(1)|λa|=______.(2)当 λ>0 时,λa 与 a的方向______;当 λ<0时,λa 与 a 的方向______;当 λ=0 时,λa=____.λ(μa)=______;(λ+μ)a=________;λ(a+b)=________.答案b+a a+(b+c) |λ||a| 相同 相反 0 λμa λa+μa λa+λb2.判断正误(1)AB+BC+CD=AD.( )(2)在△ABC 中,D 是 BC 的中点,则AD=(AC+AB).( )答案:(1)√ (2)√3.(必修④ P92 习题 2.2B 组第 5 题改编)在平行四边形 ABCD 中,若|AB+AD|=|AB-AD|,则四边形 ABCD 的形状为______...