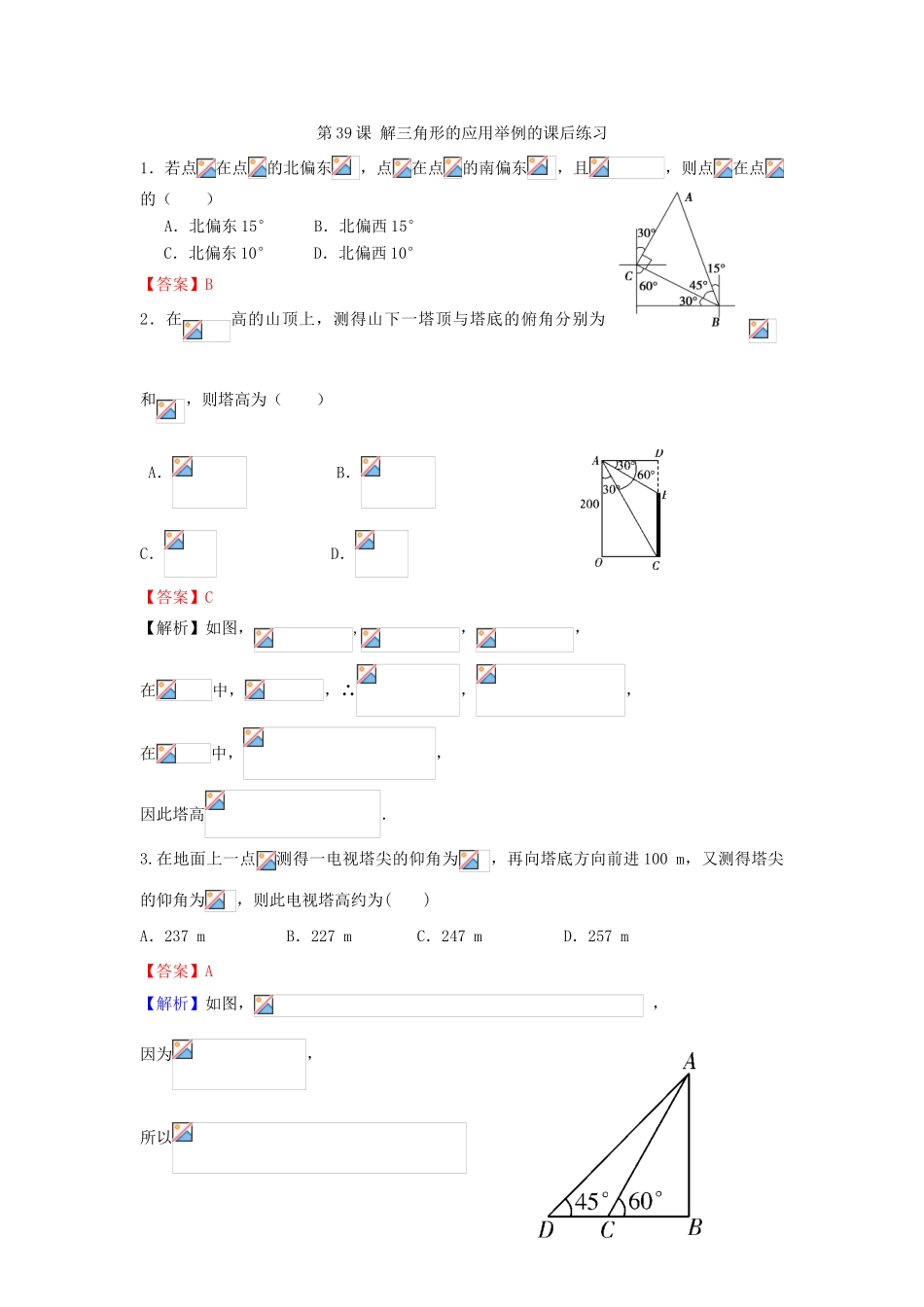
第 39 课 解三角形的应用举例1.仰角和俯角:目标视线在水平视线上方叫仰角,目标视线在水平视线下方叫俯角.2.方位角:指正北方向顺时针转到目标方向线水平角.如点的方位角为(如图⑵) .3.方向角:相对于某一正方向的水平角(如图 3)① 北偏东即由指北方向顺时针旋转到达目标方向.② 北偏西即由指北方向逆时针旋转到达目标方向.③ 南偏西等其他方向角类似.【例 1】(2013 临川模拟)如图,渔船甲位于岛屿的南偏西方向的处,且与岛屿相距 12 海里,渔船乙以 10 海里/小时的速度从岛屿出发沿正北方向航行,若渔船甲同时从处出发沿北偏东的方向追赶渔船乙,刚好用 2 小时追上.(1)求渔船甲的速度;(2)求的值.【解析】(1)依题意,,,,. 在△中,由余弦定理,得 ,解得.∴渔船甲的速度为海里/小时.(2)在中,,,,,由正弦定理,得. 即.ABC东南西北【例 2】在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市的东偏南 方向 300 km 的海面处,并以 20 km/h 的速度向西偏北 45°方向移动,台风侵袭的范围为圆形区域,当前半径为 60 km,并以 10 km/h 的速度不断增大,问几小时后该城市开始受到台风的侵袭? 【解析】设 小时后,台风移动 千米到达处,则 ,此时台风侵袭的范围以为圆心,为半径的圆的内部,若,则城市受到侵袭.因为,所以,所以.在 中,,由余弦定理得, 由 得, ,化简得 ,所以 .答:12 小时后该城市开始受到台风的侵袭.第 39 课 解三角形的应用举例的课后练习1.若点在点的北偏东,点在点的南偏东,且,则点在点的( )A.北偏东 15° B.北偏西 15°C.北偏东 10° D.北偏西 10°【答案】B2.在高的山顶上,测得山下一塔顶与塔底的俯角分别为和,则塔高为( ) A. B. C. D.【答案】C【解析】如图,,,, 在中,,∴,,在中,,因此塔高.3.在地面上一点测得一电视塔尖的仰角为,再向塔底方向前进 100 m,又测得塔尖的仰角为,则此电视塔高约为( )A.237 m B.227 m C.247 m D.257 m【答案】A【解析】如图, ,因为,所以.所以选 A.4.(2011· 上 海 卷 ) 在 相 距 2 千 米 的、两 点 处 测 量 目 标, 若 , ,则、 两点之间的距离是 千米.【答案】 【解析】由题意,,由正弦定理得,所以.5.某人向正东方向走了 ,他向右转 150°,然后朝新方向走了 ,结果他离出发点恰好为,那么 x 的值...