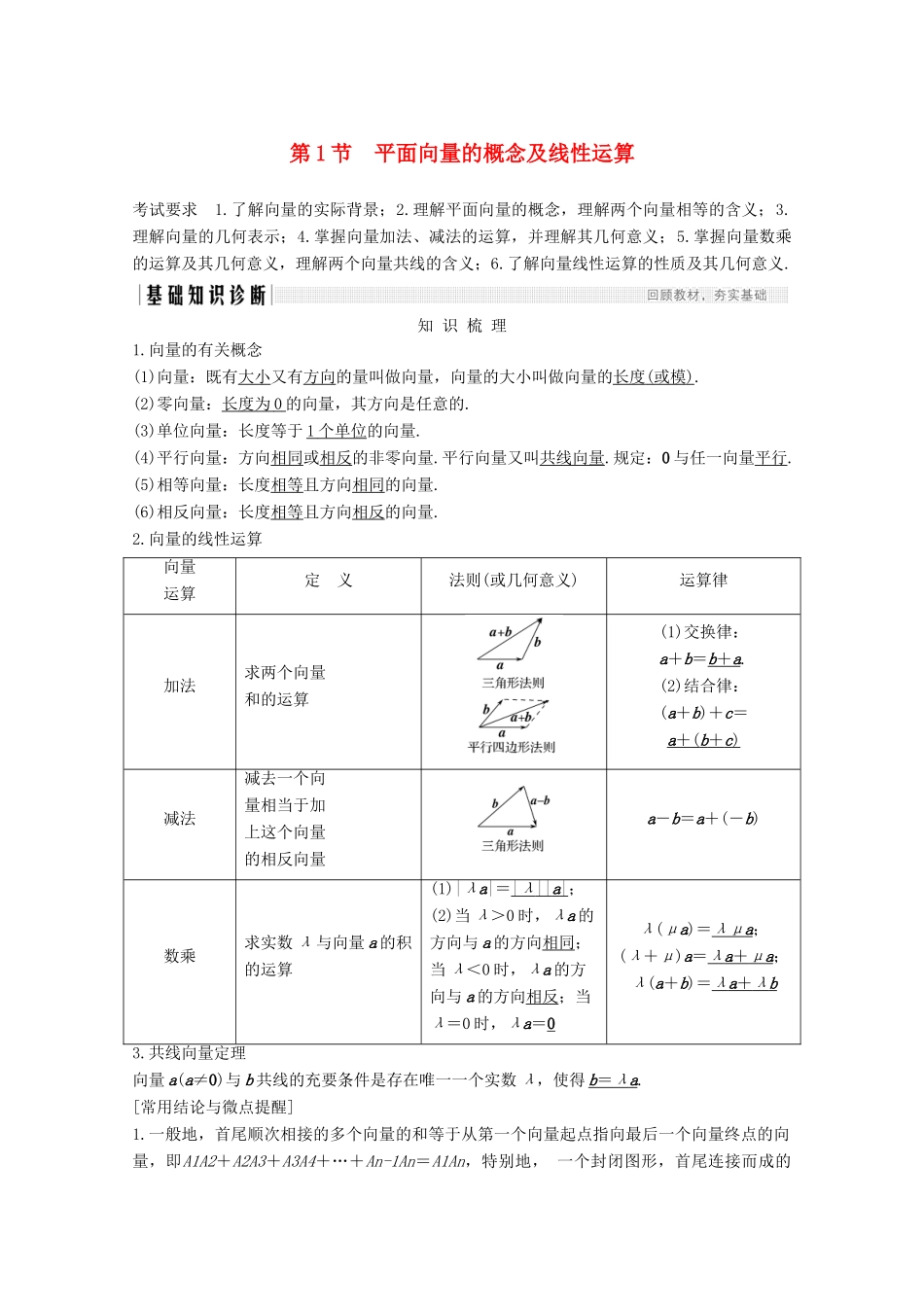
第 1 节 平面向量的概念及线性运算考试要求 1.了解向量的实际背景;2.理解平面向量的概念,理解两个向量相等的含义;3.理解向量的几何表示;4.掌握向量加法、减法的运算,并理解其几何意义;5.掌握向量数乘的运算及其几何意义,理解两个向量共线的含义;6.了解向量线性运算的性质及其几何意义.知 识 梳 理1.向量的有关概念(1)向量:既有大小又有方向的量叫做向量,向量的大小叫做向量的长度 ( 或模 ) .(2)零向量:长度为 0 的向量,其方向是任意的.(3)单位向量:长度等于 1 个单位 的向量.(4)平行向量:方向相同或相反的非零向量.平行向量又叫共线向量.规定:0 与任一向量平行.(5)相等向量:长度相等且方向相同的向量.(6)相反向量:长度相等且方向相反的向量.2.向量的线性运算向量运算定 义法则(或几何意义)运算律加法求两个向量和的运算(1)交换律:a+b=b + a .(2)结合律:(a+b)+c=a + ( b + c ) 减法减去一个向量相当于加上这个向量的相反向量a-b=a+(-b)数乘求实数 λ 与向量 a 的积的运算(1)|λa|=| λ || a | ;(2)当 λ>0 时,λa 的方向与 a 的方向相同;当 λ<0 时,λa 的方向与 a 的方向相反;当λ=0 时,λa=0λ(μa)=λμ a ;(λ+μ)a=λ a + μ a ;λ(a+b)=λ a + λ b 3.共线向量定理向量 a(a≠0)与 b 共线的充要条件是存在唯一一个实数 λ,使得 b = λ a .[常用结论与微点提醒]1.一般地,首尾顺次相接的多个向量的和等于从第一个向量起点指向最后一个向量终点的向量,即A1A2+A2A3+A3A4+…+An-1An=A1An,特别地, 一个封闭图形,首尾连接而成的向量和为零向量.2.中点公式的向量形式:若 P 为线段 AB 的中点,O 为平面内任一点,则OP=(OA+OB).3.OA=λOB+μOC(λ,μ 为实数),若点 A,B,C 共线,则 λ+μ=1.4.解决向量的概念问题要注意两点:一是不仅要考虑向量的大小,更重要的是考虑向量的方向;二是要特别注意零向量的特殊性,考虑零向量是否也满足条件.诊 断 自 测1.判断下列结论正误(在括号内打“√”或“×”)(1)|a|与|b|是否相等与 a,b 的方向无关.( )(2)若 a∥b,b∥c,则 a∥c.( )(3)向量AB与向量CD是共线向量,则 A,B,C,D 四点在一条直线上.( )(4)当两个非零向量 a,b 共线时,一定有 b=λa,反之成立.( )解析 (2)若 b=0,则 a 与 c 不一定平行.(3)共线向量所在的直线...