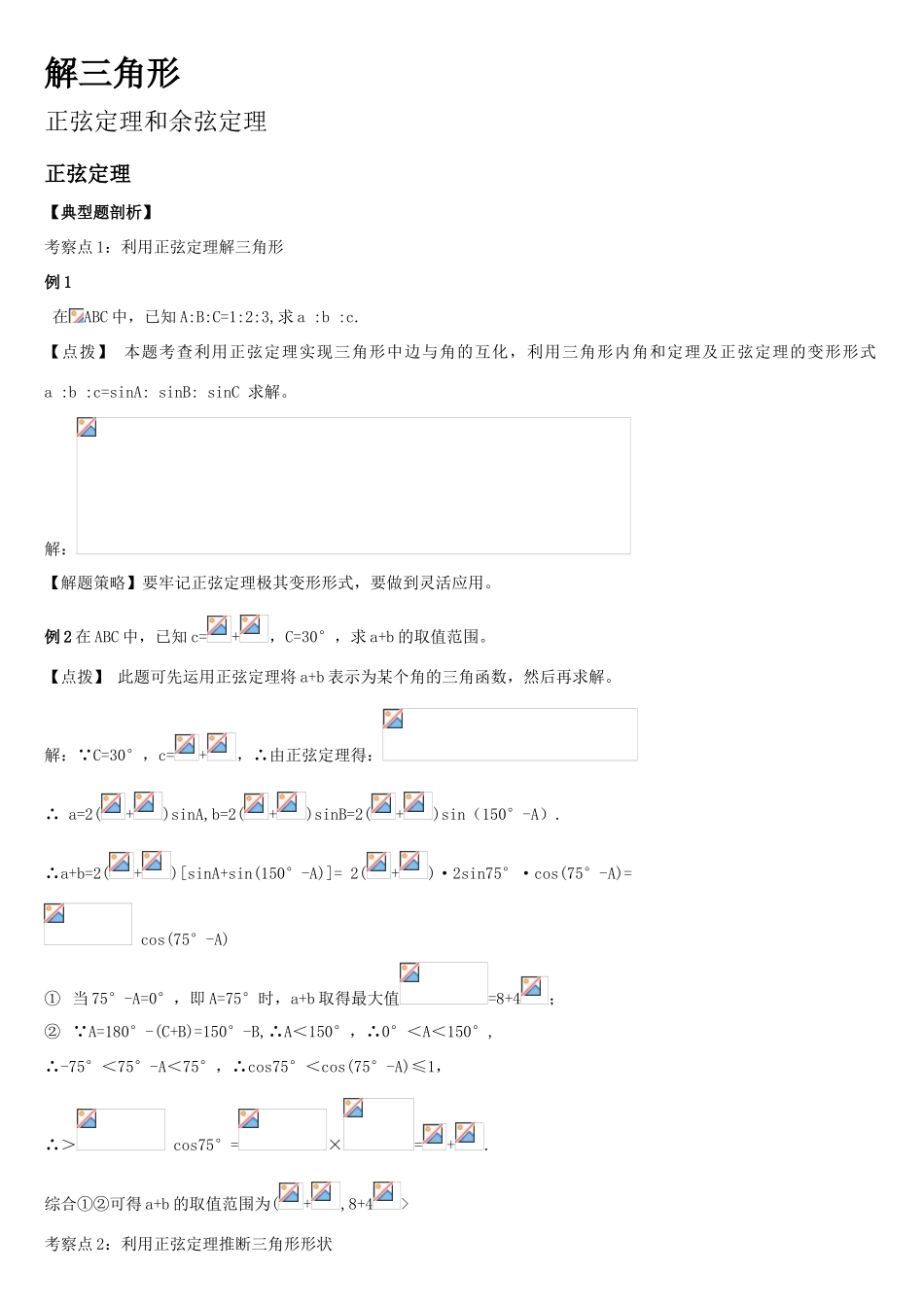
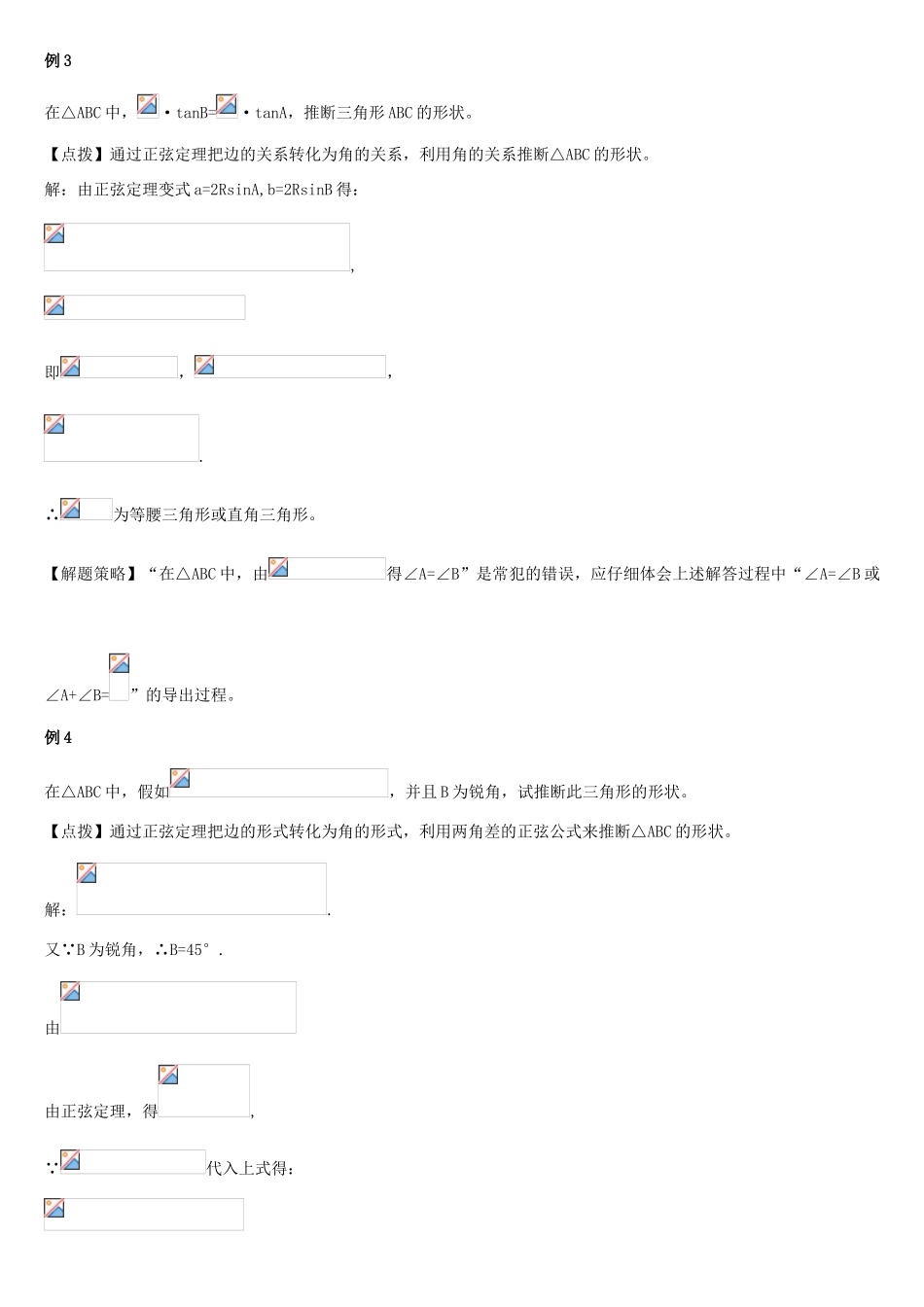
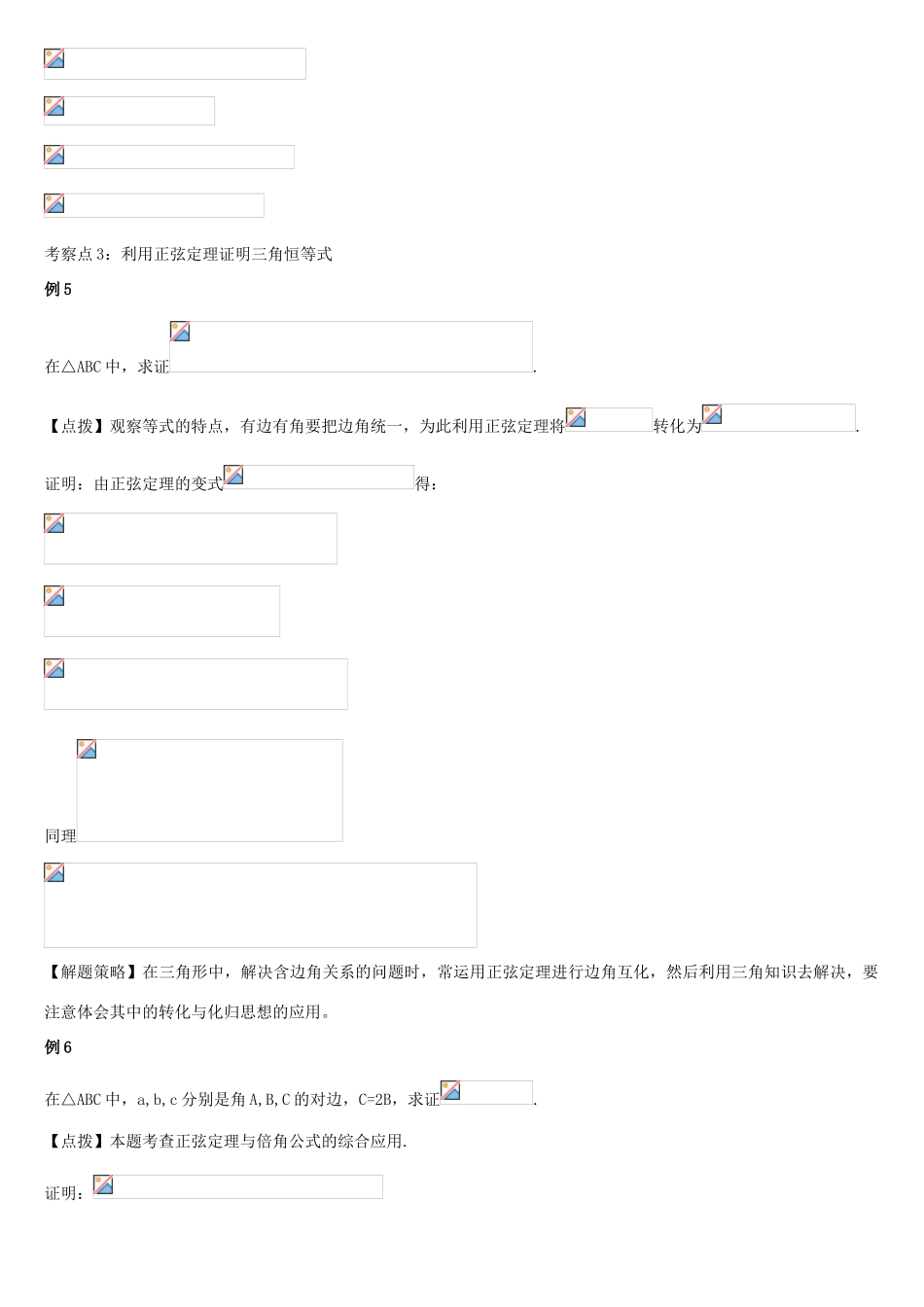
解三角形正弦定理和余弦定理正弦定理【典型题剖析】考察点 1:利用正弦定理解三角形例 1 在ABC 中,已知 A:B:C=1:2:3,求 a :b :c.【点拨】 本题考查利用正弦定理实现三角形中边与角的互化,利用三角形内角和定理及正弦定理的变形形式 a :b :c=sinA: sinB: sinC 求解。解:【解题策略】要牢记正弦定理极其变形形式,要做到灵活应用。例 2 在 ABC 中,已知 c=+,C=30°,求 a+b 的取值范围。【点拨】 此题可先运用正弦定理将 a+b 表示为某个角的三角函数,然后再求解。解: C=30°,c=+,∴由正弦定理得:∴ a=2(+)sinA,b=2(+)sinB=2(+)sin(150°-A).∴a+b=2(+)[sinA+sin(150°-A)]= 2(+)·2sin75°·cos(75°-A)= cos(75°-A)① 当 75°-A=0°,即 A=75°时,a+b 取得最大值=8+4;② A=180°-(C+B)=150°-B,∴A<150°,∴0°<A<150°,∴-75°<75°-A<75°,∴cos75°<cos(75°-A)≤1,∴> cos75°=×=+.综合①②可得 a+b 的取值范围为(+,8+4>考察点 2:利用正弦定理推断三角形形状例 3在△ABC 中,·tanB=·tanA,推断三角形 ABC 的形状。【点拨】通过正弦定理把边的关系转化为角的关系,利用角的关系推断△ABC 的形状。解:由正弦定理变式 a=2RsinA,b=2RsinB 得:,即,,.∴为等腰三角形或直角三角形。【解题策略】“在△ABC 中,由得∠A=∠B”是常犯的错误,应仔细体会上述解答过程中“∠A=∠B 或∠A+∠B=”的导出过程。例 4在△ABC 中,假如,并且 B 为锐角,试推断此三角形的形状。【点拨】通过正弦定理把边的形式转化为角的形式,利用两角差的正弦公式来推断△ABC 的形状。解:.又 B 为锐角,∴B=45°.由由正弦定理,得, 代入上式得:考察点 3:利用正弦定理证明三角恒等式例 5在△ABC 中,求证.【点拨】观察等式的特点,有边有角要把边角统一,为此利用正弦定理将转化为.证明:由正弦定理的变式得:同理【解题策略】在三角形中,解决含边角关系的问题时,常运用正弦定理进行边角互化,然后利用三角知识去解决,要注意体会其中的转化与化归思想的应用。例 6在△ABC 中,a,b,c 分别是角 A,B,C 的对边,C=2B,求证.【点拨】本题考查正弦定理与倍角公式的综合应用.证明:【解题策略】有关三角形的证明题中,要充分利用三角形本身所具有的性质。考察点 4:求三角形的面积例 7在△ABC 中,a,b,c 分别是三个内角 A,B,C 的对边,若,求△ABC 的面积 S.【点拨】先利...